题目内容
8.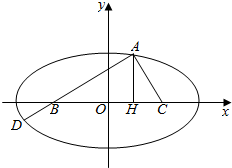 如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.
如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.
分析 由题意得到H的横坐标,设出A的坐标,再由$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,把D的坐标用A的坐标表示,然后分别把A,D的坐标代入椭圆方程,联立消去A的纵坐标求得椭圆的离心率.
解答 解:∵B(-c,0),C(c,0),
∴由$\overrightarrow{BH}$=3$\overrightarrow{HC}$,解出H($\frac{c}{2}$,0),
∵AH⊥BC,可设A($\frac{c}{2}$,y0),
再设D(x1,y1),
$\overrightarrow{AD}=({x}_{1}-\frac{c}{2},{y}_{1}-{y}_{0})$,$\overrightarrow{DB}=(-c-{x}_{1},-{y}_{1})$.
又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,
∴$({x}_{1}-\frac{c}{2},{y}_{1}-{y}_{0})=(4c+4{x}_{1},4{y}_{1})$,
∴$\left\{\begin{array}{l}{{x}_{1}-\frac{c}{2}=4c+4{x}_{1}}\\{{y}_{1}-{y}_{0}=4{y}_{1}}\end{array}\right.$,
解得:D($-\frac{3c}{2}$,$-\frac{{y}_{0}}{3}$),
将A($\frac{c}{2}$,y0),D($-\frac{3c}{2}$,$-\frac{{y}_{0}}{3}$)代入$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,
可得$\left\{\begin{array}{l}{\frac{{c}^{2}}{4{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1}\\{\frac{9{c}^{2}}{4{a}^{2}}+\frac{{{y}_{0}}^{2}}{9{b}^{2}}=1}\end{array}\right.$,消去y0得:$e=\frac{\sqrt{10}}{5}$.
点评 本题给出三角形满足的几何关系和向量等式,求椭圆的离心率.着重考查了向量的坐标运算、向量的数量积和椭圆的简单几何性质等知识,属于中档题.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | (4,3) | B. | (3,4) | C. | (3,2) | D. | (2,3) |
| A. | 充分必要条件 | B. | 充分条件但非必要条件 | ||
| C. | 必要条件但非充分条件 | D. | 既非充分条件又非必要条件 |
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |