题目内容
如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, ,
, .设
.设 ,
, 分别为
分别为 ,
, 中点.
中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)试问在线段 上是否存在点
上是否存在点 ,使得过三点
,使得过三点  ,
, ,
, 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面 平行?若存在,指出点
平行?若存在,指出点 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.

证明:
(Ⅰ)因为点 是
是 中点,点
中点,点 为
为 的中点,
的中点,
所以 ∥
∥ .
.
又因为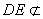 面
面 ,
, 面
面 ,
,
所以 ∥平面
∥平面 .
.
(Ⅱ)因为平面 面
面 , 平面
, 平面 平面
平面 =
= ,又
,又 平面
平面 ,
, ,所以
,所以 面
面 .
.
所以 .
.
又因为 ,且
,且 ,
,
 所以
所以 面
面 .
.
(Ⅲ)当点 是线段
是线段 中点时,过点
中点时,过点 ,
, ,
, 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面 平行.
平行.
取 中点
中点 ,连
,连 ,连
,连 .
.
由(Ⅰ)可知 ∥平面
∥平面 .
.
因为点 是
是 中点,点
中点,点 为
为 的中点,
的中点,
所以 ∥
∥ .
.
又因为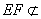 平面
平面 ,
, 平面
平面 ,
,
所以 ∥平面
∥平面 .
.
又因为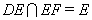 ,
,
所以平面 ∥平面
∥平面 ,
,
所以平面 内的任一条直线都与平面
内的任一条直线都与平面 平行.
平行.
故当点 是线段
是线段 中点时,过点
中点时,过点 ,
, ,
, 所在平面内的任一条直线都与平面
所在平面内的任一条直线都与平面 平行.
平行.

练习册系列答案
相关题目
 轴正半轴上一点
轴正半轴上一点 ,作圆
,作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则
,则 的最小值为( )
的最小值为( ) C.2 D.3
C.2 D.3 :
: 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆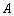 满足
满足 . 若点
. 若点 是椭圆
是椭圆 的最大值为
的最大值为 B.
B.  C.
C.  D.
D. 
 满足
满足 ,则
,则 的最小值为
的最小值为  B.
B.  C.
C.  D.
D. 
 :
: 被圆
被圆
 截得的弦
截得的弦 R,
R, ”的否定是( )
”的否定是( ) B.不存在
B.不存在 R,
R,  R,
R, 实数,且y=x}, 则A ∩ B的子集个数为_______.
实数,且y=x}, 则A ∩ B的子集个数为_______.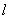 与圆
与圆 相交于
相交于 ,
, 两点,且线段
两点,且线段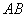 的中点坐标是
的中点坐标是 ,则直线
,则直线 函数
函数 在
在 上单调递增;命题
上单调递增;命题 不等式
不等式 的解集是
的解集是 .若
.若 且
且 为真命题,则实数
为真命题,则实数 的取值范围是______.
的取值范围是______.