题目内容
19.某几何体的三视图如图所示,则该几何体的外接球的半径为( )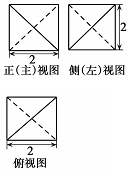
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
分析 由已知中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,进而得到答案.
解答 解:由已知中的三视图可得:
该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,
其外接球等同于棱长为2的正方体的外接球,
故2R=$\sqrt{{2}^{2}+{2}^{2}+{2}^{2}}$=2$\sqrt{3}$,
故R=$\sqrt{3}$,
故选:B
点评 三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
9.某百货公司1~6月份的销售量x与利润y的统计数据如表:
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$)=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$.
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
| 利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$)=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$.
10.已知等比数列{an}中,an+1=36,an+3=m,an+5=4,则圆锥曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{3}$=1的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{5}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
14.若cos($\frac{π}{2}+α$)=$\frac{3}{5}$,则cos2α=( )
| A. | $-\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | 一$\frac{16}{25}$ | D. | $\frac{16}{25}$ |
11.阅读如图的程序框图,运行相应的程序,则输出的值为( )
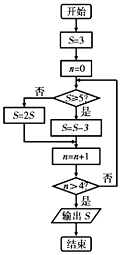

| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
9.已知函数f(x)=ex+$\frac{2x-5}{{x}^{2}+1}$的图象在点(0,f(0))处的切线与直线x-my+4=0垂直,则实数m的值为( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
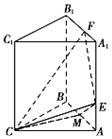 在三棱柱ABC-A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=$\frac{1}{2}$,A1F=$\frac{3}{4}$,CE⊥EF,M为AB中点
在三棱柱ABC-A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=$\frac{1}{2}$,A1F=$\frac{3}{4}$,CE⊥EF,M为AB中点