题目内容
3.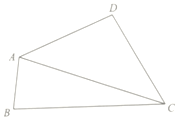 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,(Ⅰ)求 cos∠DAC 及AC 的长;
(Ⅱ)求BC的长.
分析 (Ⅰ)根据余弦定理和夹角公式计算即可;
(Ⅱ)根据同角的三角函数的关系,二倍角公式诱导公式两角和与差的正弦公式,以及正弦定理即可求出.
解答 解:(Ⅰ)由余弦定理可得AC2=AD2+DC2-2AD•DC•cosD=4+4-2×2×2×(-$\frac{1}{7}$)=$\frac{64}{7}$,
即AC=$\frac{8\sqrt{7}}{7}$,
则cos∠DAC=$\frac{A{D}^{2}+A{C}^{2}-D{C}^{2}}{2•AD•AC}$=$\frac{\frac{64}{7}+4-4}{2×\frac{8\sqrt{7}}{7}×2}$=$\frac{2\sqrt{7}}{7}$;
(Ⅱ)由(Ⅰ)cos∠DAC=$\frac{2\sqrt{7}}{7}$,
∴sin∠DAC=$\frac{\sqrt{21}}{7}$
∴sinB=sin(∠BAC+∠ACB)=sin(120°-∠DAC+60°-∠DCA)
=sin(∠DAC+∠DCA)=sin(2∠DAC)=2sin∠DAC•cos∠DAC=2×$\frac{2\sqrt{7}}{7}$×$\frac{\sqrt{21}}{7}$=$\frac{4\sqrt{3}}{7}$,
∴sin∠BAC=sin(120°-∠DAC)=$\frac{\sqrt{3}}{2}$×$\frac{2\sqrt{7}}{7}$+$\frac{1}{2}$×$\frac{\sqrt{21}}{7}$=$\frac{3\sqrt{21}}{14}$,
∴sinB=sin(∠BAC+∠ACB)=$\frac{3\sqrt{21}}{14}$×$\frac{5\sqrt{7}}{14}$+$\frac{\sqrt{7}}{14}$×$\frac{\sqrt{21}}{14}$=$\frac{4\sqrt{3}}{7}$,
由正弦定理可得$\frac{BC}{sin∠BAC}$=$\frac{AC}{sinB}$,
∴BC=$\frac{\frac{8\sqrt{7}}{7}×\frac{3\sqrt{21}}{14}}{\frac{4\sqrt{3}}{7}}$=3.
点评 本题考查了同角的三角函数的关系,二倍角公式诱导公式两角和与差的正弦公式,以及正弦定理、余弦定理,考查了学生的运算能力,属于中档题.

| A. | (-∞,9] | B. | (0,9] | C. | [0,9] | D. | [0,9) |
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 3π |
 执行右面的程序框图,则输出的B=( )
执行右面的程序框图,则输出的B=( )| A. | 31 | B. | 63 | C. | 127 | D. | 255 |
 根据如图所示的伪代码,当输入x的值为e(e为自然对数的底数)时,则输出的y的值为1.
根据如图所示的伪代码,当输入x的值为e(e为自然对数的底数)时,则输出的y的值为1.