题目内容
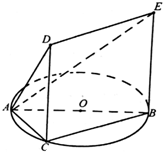 如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.(Ⅰ)证明:AD⊥BC
(Ⅱ)若AB=4,BC=2,且二面角A-BD-C所成角θ的正切值是2,试求该几何体ABCDE的体积.
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)利用圆的性质可得AC⊥BC,已知DC⊥平面ABC,可得DC⊥BC,可得BC⊥平面ACD,再利用线面垂直的性质即可得出;
(II)设CD=a,以CB,CA,CD所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图所示.由(Ⅰ)可得,AC⊥平面BCD,可得平面BCD的一个法向量是
=(0,2
,0),设
=(x,y,z)为平面ABD的一个法向量,利用
,即可得出
.又二面角A-BD-C所成角θ的正切值是2,可得cosθ=
.|cos<
,
>|=cosθ=
,解得a.利用VABCDE=VE-ADC+VE-ABC=
S△ADC•|ED|+
S△ABC•|EB|,即可得出.
(II)设CD=a,以CB,CA,CD所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图所示.由(Ⅰ)可得,AC⊥平面BCD,可得平面BCD的一个法向量是
| CA |
| 3 |
| n |
|
| n |
| ||
| 5 |
| n |
| CA |
|
| ||||
|
|
| 1 |
| 3 |
| 1 |
| 3 |
解答:
(Ⅰ)证明:∵AB是圆O的直径,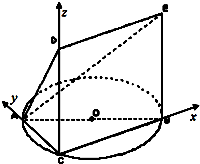
∴AC⊥BC,
又∵DC⊥平面ABC
∴DC⊥BC,
又AC∩CD=C,
∴BC⊥平面ACD,
又AD?平面ACD,
∴AD⊥BC.
(Ⅱ)解:设CD=a,以CB,CA,CD所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图所示.
则C(0,0,0),B(2,0,0),A(0,2
,0),D(0,0,a).
由(Ⅰ)可得,AC⊥平面BCD,
∴平面BCD的一个法向量是
=(0,2
,0),
设
=(x,y,z)为平面ABD的一个法向量,
由条件得,
=(2,-2
,0),
=(-2,0,a).
∴
即
,
不妨令x=1,则y=
,z=
,
∴
=(1,
,
).
又二面角A-BD-C所成角θ的正切值是2,
∴cosθ=
.
∴|cos<
,
>|=cosθ=
,
∴
=
=
,解得a=2
.
∴VABCDE=VE-ADC+VE-ABC
=
S△ADC•|ED|+
S△ABC•|EB|
=
×|AC|×|DC|×|ED|+
×|AC|×|BC|×|EB|
=
×2
×2
×2+
×2
×2×2
=8.
∴该几何体ABCDE的体积是8.

∴AC⊥BC,
又∵DC⊥平面ABC
∴DC⊥BC,
又AC∩CD=C,
∴BC⊥平面ACD,
又AD?平面ACD,
∴AD⊥BC.
(Ⅱ)解:设CD=a,以CB,CA,CD所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图所示.
则C(0,0,0),B(2,0,0),A(0,2
| 3 |
由(Ⅰ)可得,AC⊥平面BCD,
∴平面BCD的一个法向量是
| CA |
| 3 |
设
| n |
由条件得,
| AB |
| 3 |
| AD |
∴
|
|
不妨令x=1,则y=
| ||
| 3 |
| 2 |
| a |
∴
| n |
| ||
| 3 |
| 2 |
| a |
又二面角A-BD-C所成角θ的正切值是2,
∴cosθ=
| ||
| 5 |
∴|cos<
| n |
| CA |
| ||
| 5 |
∴
|
| ||||
|
|
|2
| ||||||||||
2
|
| ||
| 5 |
| 3 |
∴VABCDE=VE-ADC+VE-ABC
=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 6 |
| 1 |
| 6 |
=
| 1 |
| 6 |
| 3 |
| 3 |
| 1 |
| 6 |
| 3 |
| 3 |
=8.
∴该几何体ABCDE的体积是8.
点评:本题考查了向量相互垂直与数量积的关系证明线面垂直、利用法向量的夹角求出二面角的方法、三棱锥的体积计算公式,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知集合A={x|x2-3x+2=0},B={-2,-1,1,2},则A∩B=( )
| A、{-2,-1} |
| B、{-1,2} |
| C、{1,2} |
| D、{-2,-1,1,2} |
过点M(1,
)向抛物线C:y2=ax的准线作垂线,垂足为D,若|MD|=|MO|(其中O是坐标原点),则a=( )
| a |
| A、8 | B、4 | C、6 | D、-8或8 |
已知f(x)为奇函数,当x∈[0,1]时,f(x)=1-2|x-
|,当x∈(-∞,-1],f(x)=1-e-1-x,若关于x的不等式(x+m)>f(x)有解,则实数m的取值范围为( )
| 1 |
| 2 |
| A、(-1,0)∪(0,+∞) | ||
| B、(-2,0)∪(0,+∞) | ||
C、{-
| ||
D、{-
|
已知函数f(x)=
,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围是( )
|
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
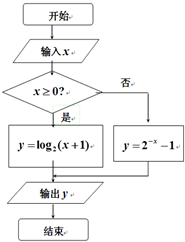
如图所示的程序框图的输出值y∈(1,2],则输入值x的范围是( )

| A、(-∞,3] |
| B、[-1,log23) |
| C、[-log23,-1)∪(1,3] |
| D、[-log23,0)∪(1,3] |
 如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=
如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=