题目内容
 如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=
如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=| 2 |
(1)求证:EC⊥平面BDF;
(2)求二面角E-BD-F的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)以点A为坐标原点,AD所在的直线为x轴,AB所在直线为y轴,AE所在直线为z轴建立直角坐标系,只要证明
•
=0,
•
=0,即可证明EC⊥平面BDF;
(2)由(1)知向量
为平面BDF的法向量,设平面EBD的法向量为
=(x,y,z),利用
,即可得出,再利用向量的夹角公式即可得出.
| EC |
| BD |
| EC |
| BF |
(2)由(1)知向量
| EC |
| n |
|
解答:
(1)证明:以点A为坐标原点,AD所在的直线为x轴,AB所在直线为y轴,AE所在直线为z轴建立直角坐标系,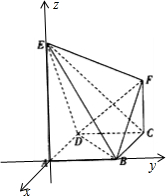
则A(0,0,0),B(0,
,0),D(-
,0,0),C(-
,
,0),F(-
,
,1),E(0,0,2),
∴
=(-
,-
,0),
=(-
,0,1),
=(-
,
,-2),
从而有
•
=0,
•
=0,
∴EC⊥BD,EC⊥BF,
又∵BD∩BF=B,从而EC⊥面BDF.
(2)解:由(1)知向量
为平面BDF的法向量,
设平面EBD的法向量为
=(x,y,z),
则
,即
;
令z=1得x=-
,y=
,
故 cos<
,
>=
=
=
,
∴二面角E-BD-F的余弦值为
.

则A(0,0,0),B(0,
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴
| BD |
| 2 |
| 2 |
| BF |
| 2 |
| EC |
| 2 |
| 2 |
从而有
| EC |
| BD |
| EC |
| BF |
∴EC⊥BD,EC⊥BF,
又∵BD∩BF=B,从而EC⊥面BDF.
(2)解:由(1)知向量
| EC |
设平面EBD的法向量为
| n |
则
|
|
令z=1得x=-
| 2 |
| 2 |
故 cos<
| n |
| EC |
| ||||
|
|
| 2 | ||
2
|
| ||
| 10 |
∴二面角E-BD-F的余弦值为
| ||
| 10 |
点评:本题考查了向量相互垂直与数量积的关系证明线面垂直、利用法向量的夹角求出二面角的方法,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
定义域为R的函数f(x)满足f(x+2)=2f(x)-2,当x∈(0,2]时,f(x)=
,若x∈(0,4]时,t2-
≤f(x)恒成立,则实数t的取值范围是( )
|
| 7t |
| 2 |
| A、[1,2] | ||
B、[2,
| ||
C、[1,
| ||
| D、[2,+∞) |
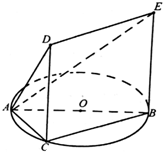 如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.