题目内容
已知f(x)为奇函数,当x∈[0,1]时,f(x)=1-2|x-
|,当x∈(-∞,-1],f(x)=1-e-1-x,若关于x的不等式(x+m)>f(x)有解,则实数m的取值范围为( )
| 1 |
| 2 |
| A、(-1,0)∪(0,+∞) | ||
| B、(-2,0)∪(0,+∞) | ||
C、{-
| ||
D、{-
|
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数的奇偶性求出函数f(x)的解析式,然后作出函数的图象,对m进行分类讨论进行求解即可.
解答:
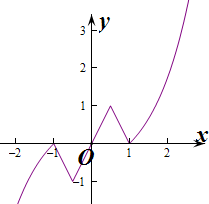 解:若x∈[-1,0],则-x∈[0,1],
解:若x∈[-1,0],则-x∈[0,1],
则f(-x)=1-2|-x-
|=1-2|x+
|,
∵f(x)是奇函数,
∴f(-x)=1-2|x+
|=-f(x),
则f(x)=2|x+
|-1,x∈[-1,0],
若x∈[1,+∞),则-x∈(-∞,-1],
则f(-x)=1-e-1+x=-f(x),
则f(x)=e-1-x-1,x∈[1,+∞),
作出函数f(x)的图象如图:
当m>0时,x+m>x,此时当x≥1时,不等式成立.
当m<0时,x+m<x,
①当x≥1时,有1+m≤x+m,不等式有解只需要1+m>0即可,解得m>-1,
②当0≤x<1时,有m≤x+m<1+m,不等式有解,只需1+m>0即可,解得m>-1,
③当-1<x<0时,有m-1<x+m<m,不等式有解,只需m>-1即可,
④当x≤-1时,有x+m<m-1<-1,此时不等式一定无解,
综上m的取值范围是(-1,0)∪(0,+∞),
故选:A
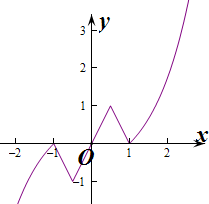 解:若x∈[-1,0],则-x∈[0,1],
解:若x∈[-1,0],则-x∈[0,1],则f(-x)=1-2|-x-
| 1 |
| 2 |
| 1 |
| 2 |
∵f(x)是奇函数,
∴f(-x)=1-2|x+
| 1 |
| 2 |
则f(x)=2|x+
| 1 |
| 2 |
若x∈[1,+∞),则-x∈(-∞,-1],
则f(-x)=1-e-1+x=-f(x),
则f(x)=e-1-x-1,x∈[1,+∞),
作出函数f(x)的图象如图:
当m>0时,x+m>x,此时当x≥1时,不等式成立.
当m<0时,x+m<x,
①当x≥1时,有1+m≤x+m,不等式有解只需要1+m>0即可,解得m>-1,
②当0≤x<1时,有m≤x+m<1+m,不等式有解,只需1+m>0即可,解得m>-1,
③当-1<x<0时,有m-1<x+m<m,不等式有解,只需m>-1即可,
④当x≤-1时,有x+m<m-1<-1,此时不等式一定无解,
综上m的取值范围是(-1,0)∪(0,+∞),
故选:A
点评:本题主要考查函数奇偶性和单调性的应用,求出函数的解析式以及利用数形结合是解决本题的关键.

练习册系列答案
相关题目
已知定义在R上的奇函数f(x),满足f(x-4)=-f(x)且在区间[0,2]上是增函数,则( )
| A、f(-25)<f(11)<f(80) |
| B、f(80)<f(11)<f(-25) |
| C、f(11)<f(80)<f(-25) |
| D、f(-25)<f(80)<f(11) |
已知命题p:?x0∈R,cosx0≤
,则?p是( )
| 1 |
| 2 |
A、?x0∈R,cosx0≥
| ||
B、?x0∈R,cosx0>
| ||
C、?x∈R,cosx≥
| ||
D、?x∈R,cosx>
|
学校组织同学参加社会调查,某小组共有5名男同学,4名女同学.现从该小组中选出3位同学分别到A,B,C三地进行社会调查,若选出的同学中男女均有,则不同安排方法有( )
| A、70种 | B、140种 |
| C、840种 | D、420种 |
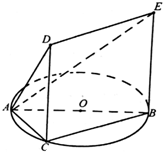 如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.