题目内容
已知
⊥
,求(
-
)•(
-
)=0.求|
|最大值.
| a |
| b |
| a |
| c |
| b |
| c |
| c |
考点:平面向量数量积的运算,向量的模
专题:平面向量及应用
分析:作
=
,
=
,
=
,由
⊥
,(
-
)•(
-
)=0.可得点C在以|
|为直径的圆上.即可得出|
|最大值为圆的直径.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| AB |
| c |
解答:
解:作
=
,
=
,
=
,
∵
⊥
,(
-
)•(
-
)=0.
∴点C在以|
|为直径的圆上.
∴|
|最大值=|
|=|
-
|.
| OA |
| a |
| OB |
| b |
| OC |
| c |

∵
| a |
| b |
| a |
| c |
| b |
| c |
∴点C在以|
| AB |
∴|
| c |
| AB |
| a |
| b |
点评:本题考查了向量垂直与数量积的关系、圆的性质、向量的三角形法则,考查了推理能力、数形结合的能力,属于中档题.

练习册系列答案
相关题目
已知集合M={x|
≥1},N={y|y=
},则M∩N=( )
| 1 |
| x |
| 1-x2 |
| A、(0,1) |
| B、[0,1] |
| C、[0,1) |
| D、(0,1] |
若等边△ABC的边长为2
,平面内一点M满足:
=
+
,则
•
=( )
| 3 |
| CM |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| MA |
| MB |
| A、-1 | B、2 | C、-2 | D、3 |
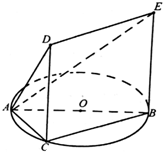 如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.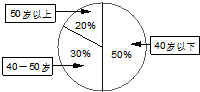 某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )
某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )