题目内容
已知sin（3π+θ）=
，求
+
．
| 1 |
| 3 |
| cos(π+θ) |
| cosθ[cos(π-θ)-1] |
| cos(θ-2π) |
| cos(θ-π)cos(-θ)-cos(9π+θ) |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：利用打官司化简已知条件，化简所求表达式代入求解即可．
解答：
解：sin（3π+θ）=
，sinθ=-
，cosθ=±
+
=
+
=
+
=
=
=
=±6
．
| 1 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| cos(π+θ) |
| cosθ[cos(π-θ)-1] |
| cos(θ-2π) |
| cos(θ-π)cos(-θ)-cos(9π+θ) |
=
| -cosθ |
| -cosθ(cosθ+1) |
| -cosθ |
| -cosθcosθ+cosθ |
=
| 1 |
| cosθ+1 |
| 1 |
| cosθ-1 |
=
| 2cosθ |
| cos2θ-1 |
=
| 2cosθ |
| -sin2θ |
=
±
| ||||
-
|
=±6
| 2 |
点评：本题考查诱导公式已经同角三角函数的基本关系式的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
已知定义在R上的奇函数f（x），满足f（x-4）=-f（x）且在区间[0，2]上是增函数，则（ ）
| A、f（-25）＜f（11）＜f（80） |
| B、f（80）＜f（11）＜f（-25） |
| C、f（11）＜f（80）＜f（-25） |
| D、f（-25）＜f（80）＜f（11） |
已知集合M={x|
≥1}，N={y|y=
}，则M∩N=（ ）
| 1 |
| x |
| 1-x2 |
| A、（0，1） |
| B、[0，1] |
| C、[0，1） |
| D、（0，1] |
已知集合A={3，4}，集合B={1，2，3，4}，则∁BA=（ ）
| A、∅ |
| B、{3，4} |
| C、{1，2} |
| D、{1，2，3，4，5} |
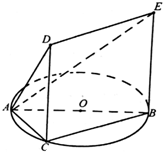如图，已知五面体ABCDE，其中△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．