题目内容
已知命题p:?x0∈R,ax02+x0+
≤0(a>0),且命题p是真命题,则a的取值范围为 .
| 1 |
| 2 |
考点:复合命题的真假
专题:简易逻辑
分析:由已知条件便可知一元二次不等式ax02+x0+
≤0有解,根据判别式△的取值情况即可求出a的取值范围.
| 1 |
| 2 |
解答:
解:根据已知条件知不等式ax02+x0+
≤0有解;
∵a>0;
∴△=1-2a≥0;
∴0<a≤
;
∴a的取值范围为(0,
].
故答案为:(0,
].
| 1 |
| 2 |
∵a>0;
∴△=1-2a≥0;
∴0<a≤
| 1 |
| 2 |
∴a的取值范围为(0,
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
点评:考查真命题的概念,知道怎么说明一个不等式有解,以及一元二次不等式的解的情况和判别式△取值的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若集合A={x||x|<1},B={x|x2-2x<0},则A∩B=( )
| A、(-1,2) |
| B、(0,1) |
| C、(0,2) |
| D、(1,2) |
如图,设全集U=R,M={x|x>2},N={0,1,2,3},则图中阴影部分所表示的集合是( )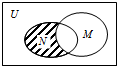

| A、{3} |
| B、{0,1} |
| C、{0,1,2} |
| D、{0,1,2,3} |