题目内容
证明|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2),并说明其几何意义.
考点:复数求模
专题:数系的扩充和复数
分析:利用复数模的运算性质即可证明,其几何意义:平行四边形的两条对角线的平方和等于四条边的平方和.
解答:
证明:左边=(z1+z2)(
+
)+(z1-z2)(
-
)
=2(z1
+z2
)
=2(|z1|2+|z2|2)=右边,
∴|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2).
其几何意义:平行四边形的两条对角线的平方和等于四条边的平方和.
. |
| z1 |
. |
| z2 |
. |
| z1 |
. |
| z2 |
=2(z1
. |
| z1 |
. |
| z2 |
=2(|z1|2+|z2|2)=右边,
∴|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2).
其几何意义:平行四边形的两条对角线的平方和等于四条边的平方和.
点评:本题考查了复数模的运算性质及其几何意义、平行四边形对角线的性质,考查了计算能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
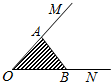 如图,A,B分别是射线OM,ON上的两点,给出下列向量:①
如图,A,B分别是射线OM,ON上的两点,给出下列向量:①| OA |
| OB |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 3 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 5 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 5 |
| OB |
| A、①② | B、②④ | C、①③ | D、③⑤ |
把边长为4、2的矩形卷成一个圆柱的侧面,其体积是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合A={x|x<a},B={x|x<3},则“a<3”是“A⊆B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
复数z=
的共轭复数
=( )
| 3-2i |
| 1-i |
. |
| z |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|