题目内容
若集合A={x||x|＜1}，B={x|x2-2x＜0}，则A∩B=（ ）
| A、（-1，2） |
| B、（0，1） |
| C、（0，2） |
| D、（1，2） |
考点：交集及其运算
专题：集合
分析：先求出不等式|x|＜1和x2-2x＜0的解集A、B，再由交集的运算求出A∩B．
解答：
解：由|x|＜1得-1＜x＜1，则集合A=（-1，1），
由x2-2x＜0得0＜x＜2，则集合B=（0，2），
所以A∩B=（0，1），
故选：B．
由x2-2x＜0得0＜x＜2，则集合B=（0，2），
所以A∩B=（0，1），
故选：B．
点评：本题考查交集及其运算，以及绝对值、二次不等式的解法，属于基础题．
练习册系列答案
相关题目
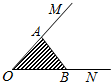如图，A，B分别是射线OM，ON上的两点，给出下列向量：①| OA |
| OB |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 3 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 5 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 5 |
| OB |
| A、①② | B、②④ | C、①③ | D、③⑤ |
把边长为4、2的矩形卷成一个圆柱的侧面，其体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|