题目内容
20.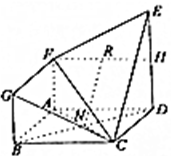 如图,在几何体ABCDEFG中,面ABCD是正方形,其对角线AC于BD相交于N,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,DE=2AF=2BG.
如图,在几何体ABCDEFG中,面ABCD是正方形,其对角线AC于BD相交于N,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,DE=2AF=2BG.(Ⅰ)若点R是FH的中点,证明:NR∥平面EFC;
(Ⅱ)若正方形ABCD的边长为2,DE=2,求二面角E-FC-G的余弦值.
分析 (Ⅰ)分别取EF、CF的中点M、Q,连MR、MQ、NQ,推导出四边形MRNQ为平行四边形,则MQ∥NR,由此能证明NR∥平面EFC.
(Ⅱ)分别以直线AB、AD、AF为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角E-FC-G的余弦值.
解答 证明:(Ⅰ)分别取EF、CF的中点M、Q,连MR、MQ、NQ,
则MR∥EH∥FA∥NQ,且MR=$\frac{1}{2}$EH=$\frac{1}{2}$FA=NQ,
∴四边形MRNQ为平行四边形,∴MQ∥NR,
又MQ?平面EFG,NR?平面EFC,
∴NR∥平面EFC.
解:(Ⅱ)分别以直线AB、AD、AF为x,y,z轴,建立空间直角坐标系,
则G(2,0,1),F(0,0,1),C(2,2,0),E(0,2,2),
∴$\overrightarrow{FG}$=(2,0,0),$\overrightarrow{CG}$=(0,-2,1),$\overrightarrow{EF}$=(0,-2,-1),$\overrightarrow{FC}$=(2,2,-1),
设平面GFC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{FG}=x=0}\\{\overrightarrow{n}•\overrightarrow{CG}=2y-z=0}\end{array}\right.$,取z=2,得$\overrightarrow{n}$=(0,1,2),
同理得平面EFC的法向量$\overrightarrow{m}$=(2,-1,2),
设二面角E-FC-G的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{3}{3\sqrt{5}}=\frac{\sqrt{5}}{5}$.
∴二面角E-FC-G的余弦值为$\frac{\sqrt{5}}{5}$.
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| 鞋码 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 合计 |
| 男生 | - | - | 3 | 6 | 8 | 11 | 12 | 6 | 7 | 2 | 55 |
| 女生 | 4 | 6 | 12 | 9 | 9 | 2 | 2 | - | - | 1 | 45 |
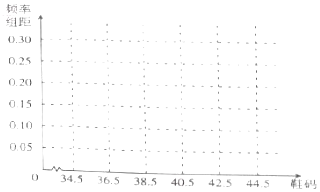
(2)完成频率分布直方图,并估计该校学生的平均鞋码.
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
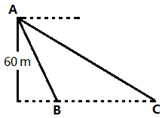 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )| A. | $30\sqrt{3}$ | B. | $30({\sqrt{3}-1})$ | C. | $40\sqrt{3}$ | D. | $40({\sqrt{3}-1})$ |