题目内容
11．已知直线x-y+2=0与圆C：（x-3）2+（y-3）2=4（圆心为C）交于点A，B，则∠ACB的大小为（ ）| A． | 30° | B． | 60° | C． | 90° | D． | 120° |
分析 求出圆心到直线的距离，利用三角函数，即可得出结论．
解答 解：由题意，圆心到直线的距离d=$\frac{|3-3+2|}{\sqrt{2}}$=$\sqrt{2}$，
圆的半径为2，∴cos$\frac{1}{2}$∠ACB=$\frac{\sqrt{2}}{2}$，∴∠ACB=90°，
故选C．
点评 本题考查点到直线距离公式，考查特殊角三角函数，比较基础．
练习册系列答案
相关题目
1．已知全集U={1，2，3，4，5}，集合M={1，4}，N={1，3，5}，则（∁UM）∪（∁UN）=（ ）
| A． | {2，4} | B． | {2，3，5} | C． | {1，3，4，5} | D． | {2，3，4，5} |
2．
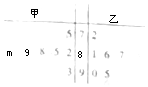甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示，两人各有一次成绩看不清楚，其中m，n∈Z，已知两位同学各自的7次成绩各不相同，但两人7次成绩的平均分相同，则两人7次成绩的中位数恰好也相同的概率为（ ）
甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示，两人各有一次成绩看不清楚，其中m，n∈Z，已知两位同学各自的7次成绩各不相同，但两人7次成绩的平均分相同，则两人7次成绩的中位数恰好也相同的概率为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{3}$ |
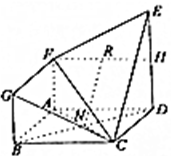如图，在几何体ABCDEFG中，面ABCD是正方形，其对角线AC于BD相交于N，DE⊥平面ABCD，DE∥AF∥BG，H是DE的中点，DE=2AF=2BG．
如图所示，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等腰梯形，等腰直角三角形和长方形，则该几何体表面积为$4\sqrt{2}$+6+$\sqrt{3}$．