题目内容
8.在遂宁市中央商务区的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、2只白色的乒乓球(其体积,质地完全相同),旁边立着一 块小黑板写道:摸球方法:从袋中随机摸出3个球,若摸得统一颜色的3个球,摊主送个摸球者5元钱;若摸得非同一颜色的3个球.摸球者付给摊主1元钱.
(1)摸出的3个球中至少有1个白球的概率是多少?
(2)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
分析 (1)摸出的3个球中至少有1个白球的对立事件是摸出的三个球都是黄球,由此利用对立事件概率公式能求出摸出的3个球中至少有1个白球的概率.
(2)设事件A={摸出的3个球为同一颜色},则P(A)=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=0.1,假定一天中有100人次摸奖,由摸出的3个球为同一颜色的概率可估计事件A发生有10次,不发生90次.由此能求出这个摊主一个月(按30天计)可赚多少钱.
解答 解:(1)摸出的3个球中至少有1个白球的对立事件是摸出的三个球都是黄球,
∴摸出的3个球中至少有1个白球的概率P=1-$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{9}{10}$.
(2)设事件A={摸出的3个球为同一颜色},
则P(A)=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=0.1,假定一天中有100人次摸奖,
由摸出的3个球为同一颜色的概率可估计事件A发生有10次,不发生90次.
则一天可赚90×1-10×5=40,
故这个摊主一个月(按30天计)可赚1200元.
点评 本题考查概率的求法及应用,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
13.某大学生从全校学生中随机选取100名统计他们的鞋码大小,得到如下数据:
以各性别各鞋码出现的频率为概率.
(1)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率;
(2)为了解该校学生考试作弊的情况,从该校随机挑选120名学生进行抽样调查.每位学生从装有除颜色外无差别的4个红球和6个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到32张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
| 鞋码 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 合计 |
| 男生 | - | - | 3 | 6 | 8 | 11 | 12 | 6 | 7 | 2 | 55 |
| 女生 | 4 | 6 | 12 | 9 | 9 | 2 | 2 | - | - | 1 | 45 |
(1)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率;
(2)为了解该校学生考试作弊的情况,从该校随机挑选120名学生进行抽样调查.每位学生从装有除颜色外无差别的4个红球和6个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到32张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
18.若函数f(x)=loga(ax-t)(a>0且a≠1)在区间[$\frac{m}{2}$,$\frac{n}{2}$]上的值域为[m,n],则实数t的取值范围是( )
| A. | (0,1) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | ($\frac{1}{2}$,1) |
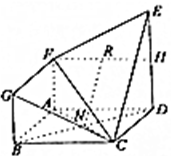 如图,在几何体ABCDEFG中,面ABCD是正方形,其对角线AC于BD相交于N,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,DE=2AF=2BG.
如图,在几何体ABCDEFG中,面ABCD是正方形,其对角线AC于BD相交于N,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,DE=2AF=2BG.