题目内容
15.已知两个正数a,b满足3a+2b=1,则$\frac{3}{a}$+$\frac{2}{b}$的最小值是( )| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
分析 根据题意,分析可得$\frac{3}{a}$+$\frac{2}{b}$=(3a+2b)($\frac{3}{a}$+$\frac{2}{b}$),对其变形可得$\frac{3}{a}$+$\frac{2}{b}$=13+($\frac{6a}{b}$+$\frac{6a}{b}$),由基本不等式分析可得答案.
解答 解:根据题意,正数a,b满足3a+2b=1,
则$\frac{3}{a}$+$\frac{2}{b}$=(3a+2b)($\frac{3}{a}$+$\frac{2}{b}$)=13+($\frac{6a}{b}$+$\frac{6a}{b}$)≥13+2$\sqrt{\frac{6a}{b}×\frac{6b}{a}}$=25;
即$\frac{3}{a}$+$\frac{2}{b}$的最小值是25;
故选:C.
点评 本题考查基本不等式的性质以及应用,关键是掌握基本不等式应用的条件.

练习册系列答案
相关题目
5.函数f(x)=3x-$\frac{4}{x}$-a的一个零点在区间(1,2)内,则实数a的取值范围( )
| A. | (-2,7) | B. | (-1,6) | C. | (-1,7) | D. | (-2,6) |
 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.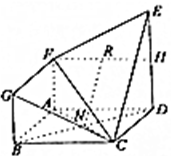 如图,在几何体ABCDEFG中,面ABCD是正方形,其对角线AC于BD相交于N,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,DE=2AF=2BG.
如图,在几何体ABCDEFG中,面ABCD是正方形,其对角线AC于BD相交于N,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,DE=2AF=2BG. 某同学收集了班里9名男生50m跑的测试成绩(单位:s):
某同学收集了班里9名男生50m跑的测试成绩(单位:s):