题目内容

已知a，b∈（0，1），M=a+b-1，N=ab，则M．N的大小关系为
 
．
考点：不等式比较大小
专题：不等式的解法及应用
分析：利用做差法，即可比较M，N的大小．
解答： 解：∵a，b∈（0，1），
∴a-1＜0，1-b＞0，
∴M-N=a+b-1-ab=a（1-b）-（1-b）=（a-1）（1-b）＜0
∴M＜N，
故答案为：M＜N
点评：本题主要考查了比较大小的方法，属于基础题．
练习册系列答案
相关题目
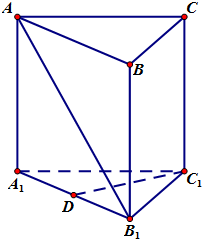从集合A={1，2，3…n}中取出r个数组成一组，若满足①数字允许重复出现②不计数字的顺序，则称其为集合A的一个r可重组合，这样的组合共有
 
．
如图，直三棱柱ABC-A1B1C1中，AC=BC=
2
，∠ACB=90°，AA1=2
3
，D是A1B1中点．
（1）求证：C1D⊥AB1；
（2）若点F是BB1上的动点，求FB1的长度，使AB1⊥面C1DF．
（x-
2
x
）6的展开式的常数项是
 
（应用数字作答）．
设数列{an}满足an+an+1=3，且前三项之和S3=4，前四项之和S4=6，则a100=（　　）
A、0B、1C、2D、3
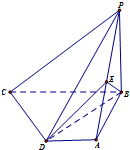在四棱锥P-ABCD中，已知PB⊥底面ABCD，BC⊥AB，AD∥BC，AB=AD=2，CD⊥BD，异面直线PA，CD所成角等于60°
（1）求证：面PCD⊥面PBD；
（2）求直线PC和平面PAD所成角的正弦值；
（3）在棱PA上是否存在一点E使得二面角A-BE-D的余弦值为
6
6
？若存在，指出E在棱PA上的位置．若不存在，说明理由．
下列四个图象中，两个变量具有正相关关系的是（　　）
A、
B、
C、
D、
已知函数f（x）=ex-
(x+1)2
2
，g（x）=2ln（x+1）+e-x．
（I）x∈（-1，+∞）时，证明：f（x）＞0；
（Ⅱ）a＞0，若g（x）≤ax+1，求a的取值范围．
已知集合A={x||x|＜1}，B={x|x＞0}，则A∩B=（　　）
A、（-1，0）
B、（-1，1）
C、（0，
1
2
）
D、（0，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网