题目内容
已知a≤1，x≥1，求证：（x+1）ln（x+1）≥ax．
考点：导数在最大值、最小值问题中的应用
专题：导数的综合应用
分析：构造函数f（x）=（x+1）ln（x+1）-ax，利用导数求其在[1，+∞）上的最小值，根据最小值大于0，即可证明不等式（x+1）ln（x+1）≥ax．
解答：
解：令f（x）=（x+1）ln（x+1）-ax，
则f′（x）=ln（x+1）+1-a，
∵x≥1，a≤1
∴ln（x+1）≥ln2＞0，1-a≥0，
∴f′（x）=ln（x+1）+1-a＞0，
∴f（x）在[1，+∞）上单调递增，
∴在[1，+∞）上f（x）≥f（1）=2ln2-a＞ln
＞0，
即（x+1）ln（x+1）-ax＞0
∴（x+1）ln（x+1）≥ax．
则f′（x）=ln（x+1）+1-a，
∵x≥1，a≤1
∴ln（x+1）≥ln2＞0，1-a≥0，
∴f′（x）=ln（x+1）+1-a＞0，
∴f（x）在[1，+∞）上单调递增，
∴在[1，+∞）上f（x）≥f（1）=2ln2-a＞ln
| 4 |
| e |
即（x+1）ln（x+1）-ax＞0
∴（x+1）ln（x+1）≥ax．
点评：本题考查利用导数求函数最值，以及最值与不等式成立的关系，属于中档题．
练习册系列答案
相关题目
若二项式（
+x2）3展开式中的常数项为k，则直线y=kx与曲线y=x2围成的封闭图形的面积为（ ）
| 1 |
| x |
| A、3 | ||
B、
| ||
| C、9 | ||
D、
|
某学校为了选拔学生参加“XX市中学生知识竞赛”，先在本校进行选拔测试（满分150分），若该校有100名学生参加选拔测试，并根据选拔测试成绩作出如图所示的频率分布直方图．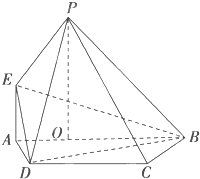
如图，PO⊥平面ABCD，点O在AB上，EA∥PO，四边形ABCD为直角梯形，BC⊥AB，BC=CD=BO=PO，EA=AO=