题目内容
 佛山某中学高三(1)班排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162、170、171、182、163、158、179、168、183、168,篮球队10人的身高(单位:cm)分别是:170、159、162、173、181、165、176、168、178、179.
佛山某中学高三(1)班排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162、170、171、182、163、158、179、168、183、168,篮球队10人的身高(单位:cm)分别是:170、159、162、173、181、165、176、168、178、179.(Ⅰ) 请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算);
(Ⅱ) 利用简单随机抽样的方法,分别在两支球队身高超过170cm的队员中各抽取一人做代表,设抽取的两人中身高超过178cm的人数为X,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,茎叶图
专题:概率与统计
分析:(Ⅰ)利用已知数据作出茎叶图,根据茎叶图能得到哪个队的身高数据方差较小.
(Ⅱ)由题设条件推导出X的所有可能取值为0,1,2,分别求出P(X=0),P(X=1),P(X=2),由此能求出X的分布列和数学期望.
(Ⅱ)由题设条件推导出X的所有可能取值为0,1,2,分别求出P(X=0),P(X=1),P(X=2),由此能求出X的分布列和数学期望.
解答:
(本题满分12分)
解:(Ⅰ)茎叶图如图所示,
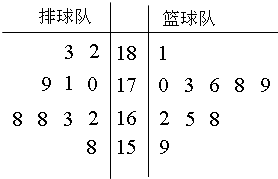
篮球队的身高数据方差较小.…(4分)
(Ⅱ)排球队中超过170cm的有4人,超过178cm的有3人,
篮球队中超过170cm的有5人,超过178cm的有2人,
所以X的所有可能取值为0,1,2…(6分)
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,…(10分)
所以X的分布列为
所以X的数学期望EX=0×
+1×
+2×
=
.…(12分)
解:(Ⅰ)茎叶图如图所示,

篮球队的身高数据方差较小.…(4分)
(Ⅱ)排球队中超过170cm的有4人,超过178cm的有3人,
篮球队中超过170cm的有5人,超过178cm的有2人,
所以X的所有可能取值为0,1,2…(6分)
P(X=0)=
| ||||
|
| 3 |
| 20 |
P(X=1)=
| ||||||||
|
| 11 |
| 20 |
P(X=2)=
| ||||
|
| 6 |
| 20 |
所以X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 3 |
| 20 |
| 11 |
| 20 |
| 6 |
| 20 |
| 23 |
| 20 |
点评:本题考查茎叶图的作法和应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组织知识的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
过点A(-2,0)的直线交圆x2+y2=1交于P、Q两点,则
•
的值为( )
| AP |
| AQ |
| A、3 | B、1 | C、5 | D、4 |
已知α是第三象限角,其终边上一点P(x,2sin
),且cosα=
x,则
sinα+tanα=( )
| 19π |
| 6 |
| ||
| 5 |
| 5 |
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
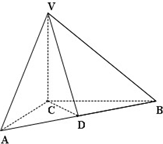 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a. 函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为
函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为