题目内容
14．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}-2\overrightarrow{b}$=0，（$\overrightarrow{a}-\overrightarrow{b}$）•$\overrightarrow{b}$=2，则|$\overrightarrow{b}$|=（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | 2 |
分析 由条件利用两个向量的数量积的定义，求得${\overrightarrow{b}}^{2}$=2，可得|$\overrightarrow{b}$|的值．
解答 解：∵向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}-2\overrightarrow{b}$=0，（$\overrightarrow{a}-\overrightarrow{b}$）•$\overrightarrow{b}$=$\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{b}}^{2}$=2${\overrightarrow{b}}^{2}$-${\overrightarrow{b}}^{2}$=${\overrightarrow{b}}^{2}$=2，则|$\overrightarrow{b}$|=$\sqrt{2}$，
故选：C．
点评 本题主要考查两个向量的数量积的定义，求向量的模的方法，属于基础题．
练习册系列答案
相关题目
4．设D为△ABC所在平面内一点，且$\overrightarrow{BC}=3\overrightarrow{BD}$，则$\overrightarrow{AD}$=（ ）
| A． | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | B． | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$ | C． | $\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D． | $\frac{2}{3}\overrightarrow{AB}+\frac{5}{3}\overrightarrow{AC}$ |
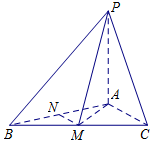在三棱锥P-ABC中，PA⊥平面ABC，AB=AC=2，BC=2$\sqrt{3}$，M，N分别为BC，AB中点．