题目内容
3.已知A,B是圆${C_1}:{x^2}+{y^2}=1$上的动点,$AB=\sqrt{3}$,P是圆${C_2}:{(x-3)^2}+{(y-4)^2}=1$上的动点,则$|{\overrightarrow{PA}+\overrightarrow{PB}}|$的取值范围为[7,13].分析 求出AB的中点的轨迹方程,即可求出$|{\overrightarrow{PA}+\overrightarrow{PB}}|$的取值范围.
解答 解:取AB的中点C,则$|{\overrightarrow{PA}+\overrightarrow{PB}}|$=2|$\overrightarrow{PC}$|,C的轨迹方程是x2+y2=$\frac{1}{4}$,|C1C2|=5
由题意,|$\overrightarrow{PC}$|最大值为5+1+$\frac{1}{2}$=$\frac{13}{2}$,最小值为5-1-$\frac{1}{2}$=$\frac{7}{2}$.
∴$|{\overrightarrow{PA}+\overrightarrow{PB}}|$的取值范围为[7,13],
故答案为[7,13].
点评 本题考查圆与圆的位置关系,考查学生的计算能力,正确转化是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
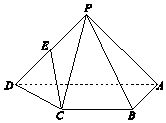 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1