Question

9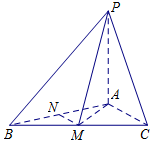．在三棱锥P-ABC中，PA⊥平面ABC，AB=AC=2，BC=2$\sqrt{3}$，M，N分别为BC，AB中点．
（I）求证：MN∥平面PAC
（II）求证：平面PBC⊥平面PAM
（III）在AC上是否存在点E，使得ME⊥平面PAC，若存在，求出ME的长，若不存在，请说明理由．

Answer 1

分析 （I）利用M，N分别为BC，AB中点，得MN∥AC，即可证明：MN∥平面PAC
（II）证明BC⊥平面PAM，即可证明：平面PBC⊥平面PAM
（III）过点M作ME⊥AC，交AC于点E，可得ME⊥平面PAC．

解答 （I）证明：因为M，N分别为BC，AB中点，
所以MN∥AC．
因为MN?平面PAC，AC?平面PAC，
所以MN∥平面PAC．…（4分）
（II）证明：因为PA⊥平面ABC，BC?平面ABC，
所以PA⊥BC．
因为AB=AC=2，M为BC的中点，
所以AM⊥BC．
因为AM∩PA=A，
所以BC⊥平面PAM．
因为BC?平面PBC，
所以平面PBC⊥平面PAM．…（8分）
（III）解：存在．
过点M作ME⊥AC，交AC于点E，
因为PA⊥平面ABC，BC?平面ABC，
所以PA⊥ME．
因为ME⊥AC，AC∩PA=A，
所以ME⊥平面PAC．
因为在△ABC中，AB=AC=2，BC=2$\sqrt{3}$，M为BC的中点，
所以ME=$\frac{\sqrt{3}}{2}$．…（13分）

点评 本题考查线面平行、垂直的判定，考查面面垂直的证明，考查学生分析解决问题的能力，属于中档题．