题目内容
4.命题p:f(x)=x3+ax2+ax在R上的单调递增函数,命题q:方程$\frac{{x}^{2}}{a+2}$+$\frac{{y}^{2}}{a-2}$=1表示双曲线.(1)当a=1时,判断命题p的真假,并说明理由;
(2)若命题“p且q“为真命题,求实数a的取值范围.
分析 (1)若命题p:f(x)=x3+ax2+ax在R上的单调递增函数为真命题,则f′(x)=3x2+2ax+a≥0恒成立,解出a的范围,可判断命题p的真假;
(2)若命题“p且q“为真命题,则命题p,命题q均为真命题,进而可得实数a的取值范围.
解答 解:(1)若命题p:f(x)=x3+ax2+ax在R上的单调递增函数为真命题,
则f′(x)=3x2+2ax+a≥0恒成立,
故△=4a2-12a≤0,
解得:a∈[0,3],
故当a=1时,命题p为真命题;
(2)若命题q:方程$\frac{{x}^{2}}{a+2}$+$\frac{{y}^{2}}{a-2}$=1表示双曲线为真命题,
则(a+2)(a-2)<0.
解得:a∈(-2,2),
若命题“p且q“为真命题,
则命题p,命题q均为真命题,
故a∈[0,2).
点评 本题以命题的真假判断与应用为载体,考查了复合命题,导数法研究函数的单调性,双曲线的标准方程等知识点,难度中档.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
14.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}-2\overrightarrow{b}$=0,($\overrightarrow{a}-\overrightarrow{b}$)•$\overrightarrow{b}$=2,则|$\overrightarrow{b}$|=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
9.若直线2x-y+2=0与直线y=kx+1平行,则实数k的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
16.已知集合A={x|$\sqrt{2x-1}$>1},则∁RA=( )
| A. | {x|x>1} | B. | {x|x≥$\frac{1}{2}$} | C. | {x|x≤1} | D. | {x|x<$\frac{1}{2}$} |
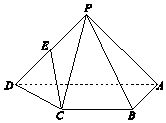 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1