题目内容
1.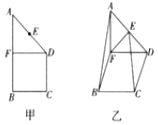 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.(1)求证:AB∥平面CEF;
(2)若二面角的余弦值为-$\frac{\sqrt{30}}{10}$,求AF的长.
分析 (Ⅰ)连接BD,FC交于点O,连接OE.由AB∥OE,得到AB∥平面CEF.
(Ⅱ)以F点为原点,FB,FD,FA分别为x,y,z轴建立空间直角
坐标系,设AF长为a,则F(0,0,0),D(0,1,0),C(1,1,0),A(0,0,a),
E(0,$\frac{1}{2}$,$\frac{a}{2}$),$\overrightarrow{FE}=(0,\frac{1}{2},\frac{a}{2}),\overrightarrow{FC}$═(1,1,0).
求出平面FEC的一个法向量、平面ECD的一个法向量,利用向量的夹角公式求出a,即可求AF的长.
解答 解:(Ⅰ)证明:如图6所示,连接BD,FC交于点O,连接OE.
因为BCDF为正方形,故O为BD中点.
又E为AD中点,故OE为△AED的中位线. …(3分)
AB∥OE,又OE?平面CEF,AB?平面CEF,
∴AB∥平面CEF. …(5分)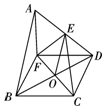
(Ⅱ)解:因为FD与AF,BF都垂直,又由题意知折为直二面角,
故AF与BF亦垂直,
故可以F点为原点,FB,FD,FA分别为x,y,z轴建立空间直角
坐标系,如图7所示.
设AF长为a,则F(0,0,0),D(0,1,0),C(1,1,0),A(0,0,a),
E(0,$\frac{1}{2}$,$\frac{a}{2}$),$\overrightarrow{FE}=(0,\frac{1}{2},\frac{a}{2}),\overrightarrow{FC}$═(1,1,0). …(7分)
设平面FEC的一个法向量为$\overrightarrow{m}=(x,y,z)$,
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{FE}=\frac{1}{2}y+\frac{a}{2}z=0}\\{\overrightarrow{m}•\overrightarrow{FC}=x+y=0}\end{array}\right.$令y=a,则$\left\{\begin{array}{l}{x=-a}\\{z=-1}\end{array}\right.$∴$\overrightarrow{m}=(-a,a,-1)$.
同理,易求平面ECD的一个法向量$\overrightarrow{n}=(0,a,1)$. …(10分)
根据题意知,cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{{a}^{2}-1}{\sqrt{2{a}^{2}+1}•\sqrt{{a}^{2}+1}}$=-$\frac{\sqrt{30}}{10}$,
解得,a=$\sqrt{7}$或a=$\frac{1}{2}$,
经分析若a=$\sqrt{7}$时,二面角余弦值应为正,故舍去.
综上,AF=$\frac{1}{2}$. …(12分)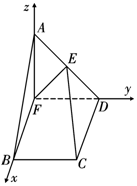
点评 本题考查了空间线面平行的判定,向量法求二面角,属于中档题.

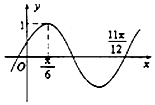 已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.
已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.