题目内容
4.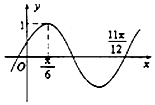 已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.
已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.
分析 首先由图象最高点横坐标与零点的距离求函数的周期,从而由周期公式求ω,然后由图象过的已知点求出a.
解答 解:由已知函数图象得到$\frac{3}{4}T=\frac{11π}{12}-\frac{π}{6}=\frac{3}{4}$π,所以T=π,所以$ω=\frac{2π}{π}$=2,
又y=f(x+a))=sinω(x+a)且($\frac{π}{6}$,1)在图象上,
所以sin2($\frac{π}{6}$+a)=1,所以$\frac{π}{3}$+2a=2kπ$+\frac{π}{2}$,k∈Z,
所以k取0时a的最小值为$\frac{π}{12}$;
故答案为:2;$\frac{π}{12}$.
点评 本题考查了由三角函数图象求函数解析式;注意几个关键点;图象与坐标轴的交点,最高点与最低点等.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
15. 某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )
某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )
 某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )
某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )| A. | 求24名男生的达标率 | B. | 求24名男生的不达标率 | ||
| C. | 求24名男生的达标人数 | D. | 求24名男生的不达标人数 |
12.某手机厂商推出一款6寸大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
19.在△ABC上,点D满足$\overrightarrow{AD}=2\overrightarrow{AB}-\overrightarrow{AC}$,则( )
| A. | 点D不在直线BC上 | B. | 点D在BC的延长线上 | ||
| C. | 点D在线段BC上 | D. | 点D在CB的延长线上 |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.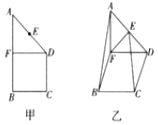 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.