题目内容
6.若数列{an}满足$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=d(n∈N*,d为常数),则称数列{an}为调和数列,现有一调和数列{bn}满足b1=1,b2=$\frac{1}{2}$.(1)求{bn}的通项公式;
(2)若数列cn=$\frac{{b}_{n}}{n+2}$,求{cn}的前n项和Sn.
分析 (Ⅰ){bn}为调和数列,故{$\frac{1}{{b}_{n}}$}为等差数列,利用等差数列的通项公式即可得出.
(Ⅱ)cn=$\frac{{b}_{n}}{n+2}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用“裂项求和”方法即可得出.
解答 解:(Ⅰ)∵{bn}为调和数列,故{$\frac{1}{{b}_{n}}$}为等差数列,
又$\frac{1}{{b}_{2}}-\frac{1}{{b}_{1}}$=1,
故{$\frac{1}{{b}_{n}}$}为等差数列,首项与公差都为1.
∴$\frac{1}{{b}_{n}}$=1+n-1=n,
故bn=$\frac{1}{n}$.…(6分)
(Ⅱ)cn=$\frac{{b}_{n}}{n+2}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,…(8分)
∴Sn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})$+$(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{3{n}^{2}+5n}{4(n+1)(n+2)}$.
点评 本题考查了等差数列通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知集合P={-1,0,1},$Q=\left\{{x\left|{y=\sqrt{x+1}}\right.}\right\}$,则P∩Q=( )
| A. | P | B. | Q | C. | {-1,1} | D. | {0,1} |
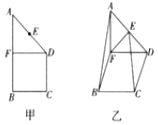 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.