题目内容
16.设实数x,y满足不等式组$\left\{\begin{array}{l}{y≥2x}\\{y-x≤1}\\{y≥1}\end{array}\right.$,则目标函数z=2x+y的最大值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先作出不等式组对应的区域,由图形判断出最优解,代入目标函数计算出最大值即可
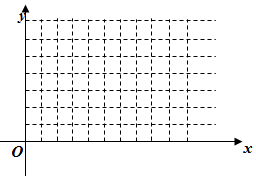
解答  解:由已知不等式组画出可行域如图,
解:由已知不等式组画出可行域如图,
目标函数z=2x+y变形为y=-2x+z,
目标函数在点A(1,2)时取得最大值,最大值为4;
故选D.
点评 本题考查简单线性规划,解题的重点是作出正确的约束条件对应的区域,根据目标函数的形式及图象作出正确判断找出最优解.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.在△ABC上,点D满足$\overrightarrow{AD}=2\overrightarrow{AB}-\overrightarrow{AC}$,则( )
| A. | 点D不在直线BC上 | B. | 点D在BC的延长线上 | ||
| C. | 点D在线段BC上 | D. | 点D在CB的延长线上 |
11. 已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
(1)求$\frac{sin∠ABD}{sin∠CBD}$;
(2)若$∠A=\frac{2π}{3}$,求BD的长.
 已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.(1)求$\frac{sin∠ABD}{sin∠CBD}$;
(2)若$∠A=\frac{2π}{3}$,求BD的长.
5. 在一次抽样调查中测得样本的5个样本点,数值如表:
在一次抽样调查中测得样本的5个样本点,数值如表:
(1)作出散点图,并判断y与x之间是否具有相关关系.若y与x非线性关系,应选择下列哪个模型更合适?(y=$\frac{k}{x}$+b,y=k•lnx+b,y=eax+b)
(2)请利用前四组数据,试建立y与x之间的回归方程.(保留小数点后1位有效数字)
 在一次抽样调查中测得样本的5个样本点,数值如表:
在一次抽样调查中测得样本的5个样本点,数值如表:| x | 0.25 | 0.5 | 1 | 2 | 4 |
| y | 16 | 12 | 5 | 2 | 1 |
(2)请利用前四组数据,试建立y与x之间的回归方程.(保留小数点后1位有效数字)
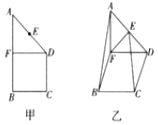 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.