题目内容
9.已知双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与圆${C_2}:{x^2}+{y^2}={c^2}$(c是双曲线的半焦距)相交于第一象限内一点P,又F1,F2分别是双曲线C1的左、右焦点,若$∠P{F_2}{F_1}=\frac{π}{3}$,则双曲线的离心率为$\sqrt{3}+1$.分析 由题意可得,三角形F1F2P是有一个内角为60°角的直角三角形,根据此直角三角形,结合双曲线的离心率的定义即可求得双曲线的离心率.
解答 解:由题设知圆C2的直径为F1F2,则$∠{F_1}P{F_2}=\frac{π}{2}$,又$∠P{F_2}{F_1}=\frac{π}{3}$,
所以$|{P{F_1}}|=\sqrt{3}c$,|PF2|=c,
由双曲线的定义得|PF1|-|PF2|=2a,即$(\sqrt{3}-1)c=2a$,所以$e=\frac{2}{{\sqrt{3}-1}}=\sqrt{3}+1$.
故答案为$\sqrt{3}+1$.
点评 本题考查双曲线的离心率,考查双曲线的定义的运用,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
12.某手机厂商推出一款6寸大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
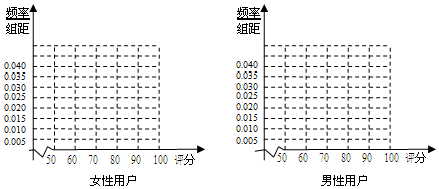
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
18.已知集合P={-1,0,1},$Q=\left\{{x\left|{y=\sqrt{x+1}}\right.}\right\}$,则P∩Q=( )
| A. | P | B. | Q | C. | {-1,1} | D. | {0,1} |
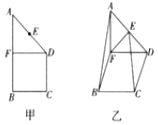 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.