Question

在椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），中，F₁，F₂分别为左右焦点A₁，A₂，B₁，B₂分别为四个顶点，已知菱形A₁B₁A₂B₂和菱形B₁F₁B₂F₂的面个积分别为4

3

和2

3

．
（1）求椭圆C的标准方程；
（2）过椭圆C的右顶点A₂作两条互相垂直的直线分别和椭圆交于另一点P，Q，试判断直线PQ是否过定点，若过定点，求出该定点的坐标；若不过定点，请说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

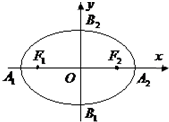
分析：（1）根据菱形A₁B₁A₂B₂和菱形B₁F₁B₂F₂的面个积分别为4

3

和2

3

，建立方程组，求出a，b，即可求椭圆C的标准方程；
（2）设直线A₂P的方程为：y=k（x-2），代入椭圆方程，消去y整理，利用韦达定理，求出P的坐标，同理求出Q的坐标，再分类讨论，求出直线PQ方程，即可得出直线PQ过定点．

解答： 解：（1）依题意知：

1 2 •2a•2b=4 3 1 2 •2c•2b=2 3 a2=b2+c2

，解得

a2=4 b2=3

，
即椭圆C的标准方程

x2

4

+

y2

3

=1．…（5分）
（2）由题意知，直线A₂P与直线A₂Q的斜率均存在且不为0，设P（x₁，y₁），Q（x₂，y₂），
设直线A₂P的方程为：y=k（x-2），直线A₂Q的方程为：y=-

1

k

（x-2）
y=k（x-2），代入椭圆方程，消去y整理可得：（4k²+3）x²-16k²x+4（4k²-3）=0，容易知△＞0恒成立，
由韦达定理得：x₁•2=

4(4k2-3)

4k2+3

，
所以x₁=

2(4k2-3)

4k2+3

，代人y=k（x-2），可得：y₁=

-12k

4k2+3

，
所以P（

2(4k2-3)

4k2+3

，

-12k

4k2+3

），
同理可得：Q（

2(4-3k2)

3k2+4

，

12k

3k2+4

），
当PQ⊥x轴时，

2(4k2-3)

4k2+3

=

2(4-3k2)

3k2+4

，解得k²=1，此时直线PQ方程为x=

2

7

，知直线PQ过点（

2

7

，0）；
当直线PQ与x轴斜交时，直线PQ的方程为：y-

12k

3k2+4

=

-7k

4(k2-1)

（x-

2(4-3k2)

3k2+4

），
化简可得：y=

-7k

4(k2-1)

（x-

2

7

），知直线PQ过定点（

2

7

，0）．
综上知，直线PQ恒过定点（

2

7

，0）．…（12分）

点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查直线方程，考查学生分析解决问题的能力，正确运用韦达定理是关键．