题目内容
如图,在△ABC中,∠B=
,AB=8,点D在BC边上,且CD=2,cos∠ADC=
.
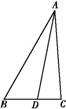
(1)求sin∠BAD;
(2)求BD,AC的长.
解:(1)在△ADC中,因为cos∠ADC=,
所以sin∠ADC=
.
所以sin∠BAD=sin(∠ADC-∠B)
=sin∠ADCcos∠B-cos∠ADCsin∠B
=×
-×
=
.
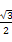
(2)在△ABD中,由正弦定理得
BD=
=
=3.
在△ABC中,由余弦定理得
AC2=AB2+BC2-2AB·BC·cos B
=82+52-2×8×5×
=49.
所以AC=7.
练习册系列答案
相关题目
,则tan 2α等于( )
(B)
(C)-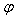
)(A>0,ω>0,| 
)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且
·
=0,则ωA=
sin xcos x-2sin2x+1.
)的值;
]上的最大值和最小值.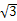
(B)2
≤A≤
=
,P是BN上的一点,若
=m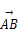
+
,则实数m的值为( )
(D)
+
的值为 . 
=
,x.y∈R..若
的夹角为
,则
的最大值等于_______.