题目内容
已知△ABC的三个内角A,B,C的对边分别为a,b,c,且△ABC的面积为S=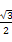 accos B.
accos B.
(1)若c=2a,求角A,B,C的大小;
(2)若a=2,且 ≤A≤
≤A≤ ,求边c的取值范围.
,求边c的取值范围.
解:由三角形面积公式及已知得S= acsin B=
acsin B=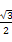 accos B,
accos B,
化简得sin B=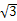 cos B,
cos B,
即tan B=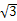 ,
,
又0<B<π,
故B= .
.
(1)由余弦定理得,b2=a2+c2-2accos B=a2+4a2-2a2=3a2,
∴b=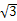 a.
a.
∴a∶b∶c=1∶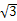 ∶2,
∶2,
知A= ,C=
,C= .
.
(2)由正弦定理得 =
= ,
,
即c= =
= ,
,
由C= -A,
-A,
得c= =
= =
= +1,
+1,
又由 ≤A≤
≤A≤ ,知1≤tan A≤
,知1≤tan A≤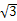 ,故c∈[2,
,故c∈[2,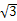 +1].
+1].

练习册系列答案
相关题目
 -α)=
-α)= ,则sin(α-
,则sin(α- )= .
)= .  ,cos B=
,cos B=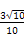 ,则tan C的值是( )
,则tan C的值是( ) ,则A等于( )
,则A等于( )
 .
.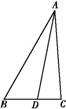
 -3
-3 +2
+2 =0,则
=0,则 的值为( )
的值为( ) (B)
(B) (C)3 (D)2
(C)3 (D)2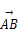 =λ
=λ +μ
+μ ,则λ+μ= .
,则λ+μ= . 
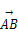 ,
, 为一组基底来表示
为一组基底来表示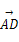 +
+ +
+ .
. =
= ,则
,则 =
= ;
;  是四边形ABCD是平行四边形的充要条件;
是四边形ABCD是平行四边形的充要条件;  ,则
,则