题目内容
已知函数f(x)=2 sin xcos x-2sin2x+1.
sin xcos x-2sin2x+1.
(1)求f( )的值;
)的值;
(2)求f(x)在区间[0, ]上的最大值和最小值.
]上的最大值和最小值.
解:(1)由f(x)=2 sin xcos x-2sin2x+1
sin xcos x-2sin2x+1
= sin 2x+cos 2x,
sin 2x+cos 2x,
得f(x)=2sin(2x+ ).
).
所以f( )=2sin
)=2sin  =
= .
.
(2)因为0≤x≤ ,所以
,所以 ≤2x+
≤2x+ ≤
≤ .
.
当2x+ =
= ,即x=
,即x= 时,
时,
函数f(x)在区间[0, ]上的最大值为2.
]上的最大值为2.
当2x+ =
= ,即x=
,即x= 时,
时,
函数f(x)在[0, ]上的最小值为-1.
]上的最小值为-1.

练习册系列答案
相关题目
 ,cos
,cos  )的值为 .
)的值为 .  个单位得到,则f(
个单位得到,则f( )等于( )
)等于( ) (B)
(B)
 (D)
(D)
 ,cos B=
,cos B=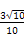 ,则tan C的值是( )
,则tan C的值是( ) ,α∈[
,α∈[ ,
, ],则cos α= .
],则cos α= .  ,则A等于( )
,则A等于( ) (B)
(B) (C)
(C) (D)
(D)
 .
.
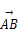 =λ
=λ +μ
+μ ,则λ+μ= .
,则λ+μ= . 
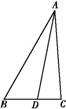
 中,
中, 点
点 为
为 的中点,点
的中点,点 在边
在边 上,若
上,若 ,则
,则 的值是 .
的值是 .