题目内容
已知2sinθ-cosθ=1,求
的值.
| sinθ+cosθ+1 |
| sinθ-cosθ+1 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式利用二倍角的正弦、余弦函数公式化简得到2sin
=cos
或cos
=0,原式利用同角三角函数间基本关系,完全平方公式,以及平方差公式变形,约分后代入计算即可求出值.
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
解答:
解:已知等式变形得:2sinθ=1+cosθ,即4sin
cos
=2cos2
,
即2sin
=cos
或cos
=0,
当2sin
=cos
时,原式=
=
=
=
=2;
当cos
=0时,原式=0.
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
即2sin
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
当2sin
| θ |
| 2 |
| θ |
| 2 |
| (sinθ+1)+cosθ |
| (sinθ+1)-cosθ |
(sin
| ||||||||
(sin
|
(sin
| ||||||||||||
(sin
|
cos
| ||
sin
|
当cos
| θ |
| 2 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
已知等差数列{an},a1=-5,前11项平均值为5,从中抽去一项,余下的平均值为4,则抽取的项为( )
| A、a11 |
| B、a10 |
| C、a9 |
| D、a8 |
幂函数y=f(x)的图象过点(4,2),那么f(
)的值为( )
| 1 |
| 16 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中,表示同一函数的一组是( )
A、f(x)=
| |||||||
| B、f(x)=lg(x(x+1)),g(x)=lgx+lg(x+1) | |||||||
| C、f(x)=x-1(x∈R),g(x)=x-1(x∈N) | |||||||
| D、f(x)=x2+x-1,g(x)=t2+t-1 |
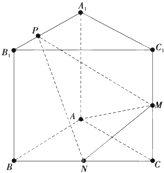 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,AB⊥AC,M、N分别是CC1、BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,AB⊥AC,M、N分别是CC1、BC的中点,点P在线段A1B1上,且