题目内容
16.如图是一个几何体的三视图,根据图中的数据,可知此几何体的表面积是( )
| A. | 24 | B. | $\frac{64}{3}$ | C. | 6+2$\sqrt{5}$+2$\sqrt{2}$ | D. | 24+8$\sqrt{5}$+8$\sqrt{2}$ |
分析 根据几何体的三视图,得出该几何体是侧面垂直于底面的直四棱锥,结合图中数据即可求出该几何体的表面积.
解答 解:根据几何体的三视图,得;
该几何体是直四棱锥,如图所示;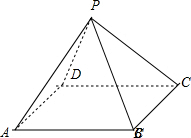
根据图中的数据,底面ABCD是边长为4的正方形,其面积为42=16;
且侧面PAB⊥底面ABCD,
又侧面PAB是等腰三角形,且高为4,其面积为$\frac{1}{2}$×4×4=8;
△PBC与△PAD的面积相等,为$\frac{1}{2}$×4×$\sqrt{{4}^{2}{+2}^{2}}$=4$\sqrt{5}$;
△PCD的面积为$\frac{1}{2}$×4×$\sqrt{{4}^{2}{+4}^{2}}$=8$\sqrt{2}$;
所以该几何体的表面积是
16+8+4$\sqrt{5}$×2+8$\sqrt{2}$=24+8$\sqrt{5}$+8$\sqrt{2}$.
故选:D.
点评 本题考查了根据几何体的三视图求表面积的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.函数f(x)=x2-x-2,x∈[-2,2],在定义域内任取一点x0,使f(x0)≤0的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
4.在一次随机试验中,彼此互斥的事件A,B,C,D的概率分别是0.2,0.1,0.3,0.4,则下列说法正确的是( )
| A. | A+B与C是互斥事件,也是对立事件 | |
| B. | B+C与D是互斥事件,也是对立事件 | |
| C. | A+C与B+D是互斥事件,但不是对立事件 | |
| D. | A与B+C+D是互斥事件,也是对立事件 |
11.已知a∈R,则“a<1”是“a2<a”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条 |
1.曲线y=$\frac{lnx-2x}{x}$在点(1,f(1))处的切线方程为( )
| A. | y=x-3 | B. | y=-x+1 | C. | y=2x-2 | D. | y=-2x+2 |
8.以等腰直角三角形ABC斜边BC上的高AD为折痕,将△ABC折成二面角C-AD-B为多大时,在折成的图形中,△ABC为等边三角形( )
| A. | 30° | B. | 60° | C. | 90° | D. | 45° |
5.已知函数f(x)=$\left\{\begin{array}{l}{2^{-x}}-0.5,x≤1\\{log_{81}}x,x>1\end{array}$,则不等式f(x)>$\frac{1}{2}$的解集为( )
| A. | (-∞,1) | B. | (-∞,0)∪(9,+∞) | C. | (9,+∞) | D. | (-∞,1)∪(9,+∞) |