题目内容
已知实数a>0 且函数f(x)=|x-2a|-|x+a|的值域为{y|-3a2≤y≤3a2
(Ⅰ)求实数a的值;
(Ⅱ)若至少存在一个实数m使得f(m)-f(1-m)≤n 成立,求实数n的取值范围.
(Ⅰ)求实数a的值;
(Ⅱ)若至少存在一个实数m使得f(m)-f(1-m)≤n 成立,求实数n的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)利用绝对值不等式得到函数的最大值和最小值;
(Ⅱ)利用函数的值域研究能成立的不等式问题,得到本题的结论.
(Ⅱ)利用函数的值域研究能成立的不等式问题,得到本题的结论.
解答:
解:(Ⅰ)∵|a-b|≥|a|-|b|,
∴|x-2a|-|x+a|=|2a-x|-|-x-a|≤|(2a-x)-(-x-a)|=|3a|.
∵实数a>0,
∴-3a≤|x-2a|-|x+a|≤3a.
∵函数f(x)=|x-2a|-|x+a|的值域为{y|-3a2≤y≤3a2},
∴
,
∴a=1.
(Ⅱ)由(Ⅰ)知a=1,
∴f(x)=|x-2|-|x+1|,
∴h(m)=f(m)-f(1-m)=|m-2|-|m+1|-|(1-m)-1|+|(1-m)+1|
=2(|m-2|-|m+1|)≥-2|(m-2)-(m+1)|=-6.
∵至少存在一个实数m使得f(m)-f(1-m)≤n 成立,
∴n≥-6.
∴|x-2a|-|x+a|=|2a-x|-|-x-a|≤|(2a-x)-(-x-a)|=|3a|.
∵实数a>0,
∴-3a≤|x-2a|-|x+a|≤3a.
∵函数f(x)=|x-2a|-|x+a|的值域为{y|-3a2≤y≤3a2},
∴
|
∴a=1.
(Ⅱ)由(Ⅰ)知a=1,
∴f(x)=|x-2|-|x+1|,
∴h(m)=f(m)-f(1-m)=|m-2|-|m+1|-|(1-m)-1|+|(1-m)+1|
=2(|m-2|-|m+1|)≥-2|(m-2)-(m+1)|=-6.
∵至少存在一个实数m使得f(m)-f(1-m)≤n 成立,
∴n≥-6.
点评:本题考查的是绝对值不等式,解题的一个难点是对能成立的不等式的正确理解.本题有一定的思维难度,属于中档题.

练习册系列答案
相关题目
若sinαtanα>0,且sinαcosα<0,则α是( )
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
(2x-1)(x+2)5的展开式中含x4项的系数( )
| A、30 | B、70 | C、90 | D、150 |
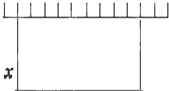 某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=
某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=