题目内容
(2x-1)(x+2)5的展开式中含x4项的系数( )
| A、30 | B、70 | C、90 | D、150 |
考点:二项式定理的应用
专题:二项式定理
分析:把(x+2)5按照二项式定理展开,可得(2x-1)(x+2)5的展开式中含x4项的系数.
解答:
解:由于(2x-1)(x+2)5=(2x-1)(x5+10x4+40x3+80x2+80x+32),
∴含x4项的系数为2×40-10=70,
故选:B.
∴含x4项的系数为2×40-10=70,
故选:B.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
已知函数f(x)周期为4,且当x∈(-1,3]时,f(x)=
,其中m>0.若方程3f(x)=x恰有5个实数解,则m的取值范围为( )
|
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
在下列各组向量中,能作为表示它们所在平面内所有向量的基底的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某次语文考试中考生的分数X~N(90,100),则分数在70~110分的考生占总考生数的百分比是( )
| A、68.26% |
| B、95.44% |
| C、99.74% |
| D、31.74% |
等差数列{an}前n项和为Sn.又a5=6,S5=20,则数列{
}前99项的和为( )
| 2 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
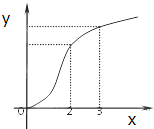

| A、0<f′(2)<f′(3)<f(3)-f(2) |
| B、0<f′(3)<f(3)-f(2)<f′(3) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-<f(2)<f′(2)<f′(3) |
已知函数f(x)=
,若方程f(x)=4有且仅有一个解,则实数a的取值范围为( )
|
| A、(0,3) |
| B、[0,3] |
| C、(1,4) |
| D、[1,4] |
已知θ是第三象限角,且sin4θ+cos4θ=
,则sinθcosθ=( )
| 5 |
| 9 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|