题目内容
8.下列命题中是假命题的是( )| A. | 存在α,β∈R,使tan(α+β)=tan α+tan β | |
| B. | 对任意x>0,有lg2x+lg x+1>0 | |
| C. | △ABC中,A>B的充要条件是sin A>sin B | |
| D. | 对任意φ∈R,函数y=sin(2x+φ)都不是偶函数 |
分析 A.存在在α=β=0,即可判断出正误;
B.对任意x>0,有lg2x+lg x+1=$(lgx+\frac{1}{2})^{2}$+$\frac{3}{4}$>0,即可判断出正误;
C.利用三角形边角关系、正弦定理,即可判断出正误;
D.取φ=$kπ+\frac{π}{2}$(k∈Z),即可判断出正误.
解答 解:A.存在在α=β=0,使tan(α+β)=tan α+tan β,是真命题;
B.对任意x>0,有lg2x+lg x+1=$(lgx+\frac{1}{2})^{2}$+$\frac{3}{4}$>0,是真命题;
C.△ABC中,A>B?a>b?sin A>sin B,是真命题;
D.取φ=$kπ+\frac{π}{2}$(k∈Z),函数y=sin(2x+φ)=±cos2x是偶函数,因此是假命题.
故选:D.
点评 本题考查了简易逻辑的判定方法、正弦定理、三角函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.如果sinα=$\frac{12}{13}$,α∈(0,$\frac{π}{2}$),那么cos(π-α)=( )
| A. | $\frac{12}{13}$ | B. | $\frac{5}{13}$ | C. | -$\frac{12}{13}$ | D. | -$\frac{5}{13}$ |
16.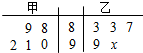 下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
 下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{4}{5}$ | D. | $\frac{9}{10}$ |
3.某单位为了了解用电量y度与气温x℃之间的关系,统计了某4天的用电量与当天气温,数据如表
由表中数据可得线性回归方程$\hat y=bx+a$中的b=-2,预测当气温为5℃时,该单位用电量的度数约为50度.
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
17.设函数f(x)=ax4+bx2-x+1(a,b∈R),若f(2)=9,则f(-2)=( )
| A. | 9 | B. | 11 | C. | 13 | D. | 不能确定 |