题目内容

已知函数f（x）=-ax3+x2-
ax
9
在（-∞，+∞）上是单调减函数，则实数a的取值范围是（　　）
A、（-∞，-
3
]∪[
3
，+∞）
B、[-
3
，
3
]
C、[
3
，+∞）
D、（-∞，
3
]
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：求出f′（x），由题意f′（x）≤0在R上恒成立，利用二次函数的性质求出a的取值范围即可得到满足题意的a范围．
解答： 解：∵f′（x）=-3ax2+2x-
a
9
，由题意f′（x）≤0在R上恒成立．
则
a＞0
△≤0
，即
a＞0
4-
4
3
a2≤0
解得a≥
3
．
故选C．
点评：此题要求学生会利用导函数的正负研究函数的单调性，是一道中档题．函数f（x）是R上的单调递减函数，则f′（x）≤0，易错误地求解成f′（x）＜0．
练习册系列答案
相关题目
在双曲线C：
x2
a2
-
y2
b2
=1中，过焦点垂直于实轴的弦长为
2
3
3
，焦点到一条渐近线的距离为1，
（1）求该双曲线的方程；
（2）若直线L：y=kx+m（m≠0，k≠0）与双曲线C交于A、B两点（A、B不是左右顶点），且以AB为直径的圆过双曲线C的右顶点．求证：直线L过定点，并求出该定点的坐标．
已知A，B，C三点不共线，空间内任一点O满足
OP
=x
OA
+y
OB
+z
OC
（x，y，z∈R），则“x+y+z=1”是“点P在由A，B，C所确定的平面内”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
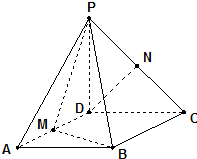已知四棱锥P-ABCD，底面ABCD是∠A=60°的菱形且PD=AD=2，又PD⊥底面ABCD，点M、N分别是棱AD、PC的中点．
（1）证明：DN∥平面PMB；
（2）证明：平面PMB⊥平面PAD；
（3）求点M到平面PBC的距离．
下列一些关于数列{an}的命题：
①若{an}既是等差数列，又是等比数列，则{an}一定是常数数列；
②若{an}是等比数列，则数列{an+an+1}一定也是等比数列；
③若{an}满足递推公式an+1=an•q，则{an}一定是等比数列；
④若{an}的前n项和Sn=qn-1，则{an}一定是等比数列．
其中正确的有
 
（填写序号）
给出下列四个命题：
①命题“?x∈R，都有x2-x+1≥
3
4
”的否定是“?x∈R，都有x2-x+1＜
3
4
”
②一个扇形的弧长与面积的数值都是5，则这个扇形中心角的弧度数是5；
③将函数y=cos2x图象向右平移
π
4
个单位，得到y=cos（2x-
π
4
）的图象；
④命题“设向量
a
=（4sinα，3），
b
=（2，cosα），若
a
∥
b
，则α=
π
4
”的逆命题、否命题、逆否命题中真命题的个数为2．
其中正确命题的序号为
 
．
已知复数z满足z•（1-i）=2-i（i为虚数单位），则复数z=
 
．
有下列五个命题：
①若A∩B=Φ，则A，B之中至少有一个为空集；
②函数y=
x(x-1)
+
x
的定义域为{x|x≥1}；
③集合A={x∈R|x2-2x+1=0}有两个元素；
④函数y=2x（x∈Z）的图象是一直线；
⑤不等式（x2-4）（x-6）2≤0的解集是{x|-2≤x≤2或x=6}．
其中错误命题的序号是
 
．
已知x与y之间的一组数据：
x0123
y1357
则y与x的线性回归方程必过点的坐标为（　　）
A、（1，2）
B、（2，3）
C、（1.5，4）
D、（1.5，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网