题目内容
给出以下几个命题,其中正确的命题有 ;(将所有正确命题的序号都填在横线上)
①由曲线y=x2与直线y=2x围成的封闭区域的面积为
;
②把5本不同的书分给4个人,每人至少1本,则不同的分法种数为
•
=480种;
③函数y=f(x)是定义在R上的偶函数,且f(x+1)=-f(x),则函数y=f(x)的图象关于直线x=1对称;
④已知f(x)是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,设a=f(ln
),b=f(log43),c=f(0.4-1.2),则c<a<b.
①由曲线y=x2与直线y=2x围成的封闭区域的面积为
| 4 |
| 3 |
②把5本不同的书分给4个人,每人至少1本,则不同的分法种数为
| A | 4 5 |
| A | 1 4 |
③函数y=f(x)是定义在R上的偶函数,且f(x+1)=-f(x),则函数y=f(x)的图象关于直线x=1对称;
④已知f(x)是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,设a=f(ln
| 1 |
| 3 |
考点:命题的真假判断与应用
专题:计算题,简易逻辑
分析:①利用定积分公式可S=
(2x-x2)dx=(x2-
x3)
=
;
②把5本不同的书分给4个人,每人至少1本,则不同的分法种数为
=240种;
③验证f(-x+1)=f(x-1)=-f(x)=f(x+1),可得结论;
④由题意f(x)=f(|x|),确定|0.4-1.2|>|ln
|>|log43|,利用f(x)在(-∞,0]上是增函数且为偶函数,f(x)在[0,+∞)上是减函数,可得结论.
| ∫ | 2 0 |
| 1 |
| 3 |
| | | 2 0 |
| 4 |
| 3 |
②把5本不同的书分给4个人,每人至少1本,则不同的分法种数为
| C | 2 5 |
| A | 4 4 |
③验证f(-x+1)=f(x-1)=-f(x)=f(x+1),可得结论;
④由题意f(x)=f(|x|),确定|0.4-1.2|>|ln
| 1 |
| 3 |
解答:
解:①曲线y=x2与直线y=2x的交点坐标为(0,0),(2,2),则S=
(2x-x2)dx=(x2-
x3)
=
,故正确;
②把5本不同的书分给4个人,每人至少1本,则不同的分法种数为
=240种,故不正确;
③函数y=f(x)是定义在R上的偶函数,且f(x+1)=-f(x),f(-x+1)=f(x-1)=-f(x)=f(x+1),则函数y=f(x)的图象关于直线x=1对称,故正确;
④由题意f(x)=f(|x|),∵log43<1,∴|log43|<1;2>|ln
|=|ln3|>1;∵|0.4-1.2|>2,∴|0.4-1.2|>|ln
|>|log43|.又∵f(x)在(-∞,0]上是增函数且为偶函数,∴f(x)在[0,+∞)上是减函数.∴c<a<b.故正确.
故答案为:①③④.
| ∫ | 2 0 |
| 1 |
| 3 |
| | | 2 0 |
| 4 |
| 3 |
②把5本不同的书分给4个人,每人至少1本,则不同的分法种数为
| C | 2 5 |
| A | 4 4 |
③函数y=f(x)是定义在R上的偶函数,且f(x+1)=-f(x),f(-x+1)=f(x-1)=-f(x)=f(x+1),则函数y=f(x)的图象关于直线x=1对称,故正确;
④由题意f(x)=f(|x|),∵log43<1,∴|log43|<1;2>|ln
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:①③④.
点评:本题考查命题的真假判断与应用,涉及知识点:定积分、排列组合、函数的对称性、单调性,难度中等.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
现有等腰三角形纸片ABC,∠A=90°,BC=2,按图示方式剪下两个正方形,则这两个正方形的面积之和的最小值为( )
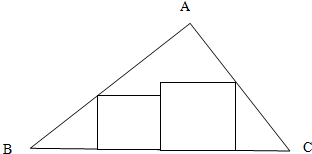

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
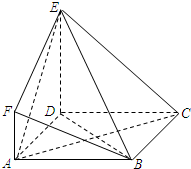 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为