题目内容
双曲线
-
=1的一条渐近线的倾斜角为α,且2cos2α=2sin2α+1,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由双曲线
-
=1的一条渐近线的倾斜角为α,可得tanα=
,从而cosα=
,sinα=
,利用2cos2α=2sin2α+1,可得a,b,c的关系,即可求出双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| a |
| c |
| b |
| c |
解答:
解:∵双曲线
-
=1的一条渐近线的倾斜角为α,
∴tanα=
,
∴cosα=
,sinα=
,
∵2cos2α=2sin2α+1,
∴2•(
)2=2•(
)2+1,
∵2a2=2(c2-a2)+c2,
∴4a2=3c2,
∴e=
=
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
∴tanα=
| b |
| a |
∴cosα=
| a |
| c |
| b |
| c |
∵2cos2α=2sin2α+1,
∴2•(
| a |
| c |
| b |
| c |
∵2a2=2(c2-a2)+c2,
∴4a2=3c2,
∴e=
| c |
| a |
2
| ||
| 3 |
故选:A.
点评:本题考查双曲线离心率的计算问题.在求双曲线的离心率时,其关键是求出c,a之间的关系,即可求出双曲线的离心率,属于基础题.

练习册系列答案
相关题目
设正弦函数f(x)=cosx在x=0和x=
处得切线得斜率分别为k1,k2,则k1,k2的大小关系为( )
| π |
| 2 |
| A、k1<k2 |
| B、k1>k2 |
| C、k1=k2 |
| D、不确定 |
现有等腰三角形纸片ABC,∠A=90°,BC=2,按图示方式剪下两个正方形,则这两个正方形的面积之和的最小值为( )
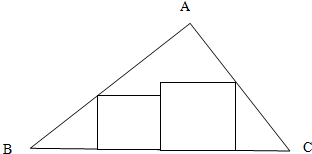

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知两不重合直线a、b及两不重合平面α、β,那么下列命题中正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
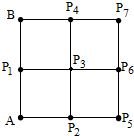 如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则
如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则| AB |
| APi |
| A、7 | B、5 | C、3 | D、1 |
如图是某空间几何体的直观图,则该几何体的侧视图是( )
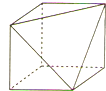

A、 |
B、 |
C、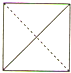 |
D、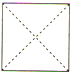 |