题目内容
下列说法正确的是( )
A、若a∈R,则“
| ||
| B、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
C、若命题p:“?x∈R,sinx+cosx≤
| ||
| D、命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3>0” |
考点:命题的真假判断与应用
专题:简易逻辑
分析:利用充要条件的定义,可判断A,B,判断原命题的真假,进而根据命题的否定与原命题真假性相反,可判断C,根据存在性(特称)命题的否定方法,可判断D.
解答:
解:若“
<1”成立,则“a>1”或“a<0”,故“
<1”是“a>1”的不充分条件,
若“a>1”成立,则“
<1”成立,故“
<1”是“a>1”的必要条件,
综上所述,“
<1”是“a>1”的必要不充分条件,故A正确;
若“p∧q为真命题”,则“p,q均为真命题”,则“p∨q为真命题”成立,
若“p∨q为真命题”则“p,q存在至少一个真命题”,则“p∧q为真命题”不一定成立,
综上所述,“p∧q为真命题”是“p∨q为真命题”的充分不必要条件,故B错误;
命题p:“?x∈R,sinx+cosx=
sin(x+
)≤
”为真命题,则¬p是假命题,故C错误;
命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3≥0”,故D错误;
故选:A.
| 1 |
| a |
| 1 |
| a |
若“a>1”成立,则“
| 1 |
| a |
| 1 |
| a |
综上所述,“
| 1 |
| a |
若“p∧q为真命题”,则“p,q均为真命题”,则“p∨q为真命题”成立,
若“p∨q为真命题”则“p,q存在至少一个真命题”,则“p∧q为真命题”不一定成立,
综上所述,“p∧q为真命题”是“p∨q为真命题”的充分不必要条件,故B错误;
命题p:“?x∈R,sinx+cosx=
| 2 |
| π |
| 4 |
| 2 |
命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3≥0”,故D错误;
故选:A.
点评:本题以命题的真假判断为载体,考查了充要条件,命题的否定等知识点,是简单逻辑的简单综合应用,难度中档.

练习册系列答案
相关题目
如图是某空间几何体的直观图,则该几何体的俯视图是( )


A、 |
B、 |
C、 |
D、 |
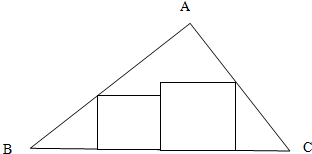
现有等腰三角形纸片ABC,∠A=90°,BC=2,按图示方式剪下两个正方形,则这两个正方形的面积之和的最小值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=x
在原点处的切线方程是( )
| 1 |
| 3 |
| A、x=0 | B、y=0 |
| C、x=0或y=0 | D、不存在 |
已知△ABC中,角A,B,C的对边是a,b,c,且a,b,c成等比数列,则函数y=sinB+cosB的取值范围是( )
A、[-
| ||||
B、(1,
| ||||
C、[1,
| ||||
D、(0,
|