题目内容
定义符号函数sgnx=
，则不等式2x+1≥xsgnx的解集是 ．
|
考点：一元二次不等式的解法
专题：新定义,不等式的解法及应用
分析：根据符号函数sgnx的定义，把不等式2x+1≥xsgnx化为能够解答的不等式即可．
解答：
解：根据题意，得；
当x＞0时，不等式为2x+1≥x，解得x≥-1，∴x＞0；
当x=0时，不等式为0+1≥00，无意义；
当x＜0时，不等式为2x+1≥x-1，即x（2x+1）≤1，解得-1≤x≤
，∴-1≤x＜0；
综上，不等式的解集是[-1，0）∪（0，+∞）．
故答案为：[-1，0）∪（0，+∞）．
当x＞0时，不等式为2x+1≥x，解得x≥-1，∴x＞0；
当x=0时，不等式为0+1≥00，无意义；
当x＜0时，不等式为2x+1≥x-1，即x（2x+1）≤1，解得-1≤x≤
| 1 |
| 2 |
综上，不等式的解集是[-1，0）∪（0，+∞）．
故答案为：[-1，0）∪（0，+∞）．
点评：本题考查了新定义的应用问题，也考查了不等式的解法与应用问题，是基础题．
练习册系列答案
活力课时同步练习册系列答案
相关题目
若等差数列{an}的公差d≠0，且a1，a3，a7成等比数列，则
=（ ）
| a1 |
| a4 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
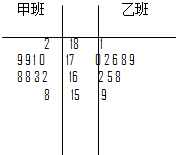最近我校对高一学生进行了体检，为了了解甲乙两班男生的身高状况，随机从甲乙两班中各抽取10名男生的身高（单位cm），绘制身高的茎叶图如图：