题目内容
已知双曲线
-
=1（a＞0，b＞0）的两条渐近线倾斜角为α，β，且sinα-cosβ=
，则双曲线离心率 ．
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 5 |
考点：双曲线的简单性质
专题：三角函数的求值,圆锥曲线的定义、性质与方程
分析：根据双曲线
-
=1（a＞0，b＞0）的两条渐近线倾斜角为α，β，且sinα-cosβ=
，求出tanα=
=
，或tanα=
=3，进而结合双曲线的性质，可得双曲线离心率．
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 5 |
| b |
| a |
| 1 |
| 3 |
| b |
| a |
解答：
解：∵双曲线
-
=1（a＞0，b＞0）的两条渐近线的倾斜角为α，β，
若α＜β，则sinα＞0，cosβ=-cosα＜0，
此时sinα-cosβ=sinα+cosα=
sin（α+
）=
，
∴sin（α+
）=
，则cos（α+
）=±
，
∴tan（α+
）=
=±2，
∴tanα=
=
，或tanα=
=3，
∴a=3b，或a=
b，
∴c=
a，或c=
a，
∴e=
，或e=
，
若α＞β，则sinα＞0，cosβ=-cosα＞0，
此时sinα-cosβ=sinα+cosα=
sin（α+
）=
，
∴sin（α+
）=
，则cos（α+
）=-
，
∴tan（α+
）=
=-2，
∴tanα=
=3，
则e=
，
综上双曲线离心率为
，或
，
故答案为：
，或
| x2 |
| a2 |
| y2 |
| b2 |
若α＜β，则sinα＞0，cosβ=-cosα＜0，
此时sinα-cosβ=sinα+cosα=
| 2 |
| π |
| 4 |
2
| ||
| 5 |
∴sin（α+
| π |
| 4 |
2
| ||
| 5 |
| π |
| 4 |
| ||
| 5 |
∴tan（α+
| π |
| 4 |
| 1+tanα |
| 1-tanα |
∴tanα=
| b |
| a |
| 1 |
| 3 |
| b |
| a |
∴a=3b，或a=
| 1 |
| 3 |
∴c=
| ||
| 3 |
| 10 |
∴e=
| ||
| 3 |
| 10 |
若α＞β，则sinα＞0，cosβ=-cosα＞0，
此时sinα-cosβ=sinα+cosα=
| 2 |
| π |
| 4 |
2
| ||
| 5 |
∴sin（α+
| π |
| 4 |
2
| ||
| 5 |
| π |
| 4 |
| ||
| 5 |
∴tan（α+
| π |
| 4 |
| 1+tanα |
| 1-tanα |
∴tanα=
| b |
| a |
则e=
| 10 |
综上双曲线离心率为
| ||
| 3 |
| 10 |
故答案为：
| ||
| 3 |
| 10 |
点评：本题考查的知识点是双曲线的简单性质，三角函数化简求值，是三角函数与圆锥曲线的综合应用，难度不大，属于基础题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
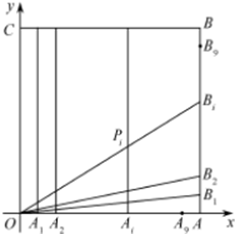如图，在正方形OABC中，O为坐标原点，点A的坐标为（10，0），点C的坐标为（0，10），分别将线段OA和AB十等分，分点分别记为A1，A2，…，A9和B1，B2，…，B9，连接OBi，过Ai作x轴的垂线与OBi，交于点Pi（i∈N*，1≤i≤9）．
如图，分别以正方形ABCD的四条边为直径画半圆，重叠部分如图中阴影区域，若向该正方形内随机投一点，则该点落在空白区域的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
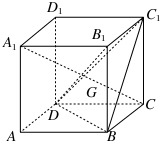如图，在棱长为a的正方体ABCD-A1B1C1D1中，G为△BC1D的重心，