题目内容
函数y=f(x)为定义在R上的增函数,对任意x,y∈R都有f(x+y)=f(x)+f(y).当a>0时,求满足不等式f(ax2+2)+f((-2a-1)x)<0的x的取值范围.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:令x=y=0可得,f(0)=f(0)+f(0),变形可得f(0)=0,再令y=-x,得f(x-x)=f(x)+f(-x),由此可得函数为奇函数,
由f(x)的奇偶性与单调性,可将原不等式变形解得x的取值范围.
由f(x)的奇偶性与单调性,可将原不等式变形解得x的取值范围.
解答:
解:在f(x+y)=f(x)+f(y)中,令x=y=0可得,f(0)=f(0)+f(0),则f(0)=0,
令y=-x,得f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x),可证得f(x)为奇函数;
因为f(x)在R上时增函数,又f(x)是奇函数,
∴不等式f(ax2+2)+f((-2a-1)x)<0可化为:f(ax2+2)<-f((-2a-1)x)=f((2a+1)x),
即ax2+2<(2a+1)x,
∴ax2-(2a+1)x+2<0,
由于a>0,且方程ax2-(2a+1)x+2=0的两根为x=2或x=
,
∴当
<2,即a>
时,ax2-(2a+1)x+2<0的解集为(
,2);
当
>2,即0<a<
时,ax2-(2a+1)x+2<0的解集为(2,
);
令y=-x,得f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x),可证得f(x)为奇函数;
因为f(x)在R上时增函数,又f(x)是奇函数,
∴不等式f(ax2+2)+f((-2a-1)x)<0可化为:f(ax2+2)<-f((-2a-1)x)=f((2a+1)x),
即ax2+2<(2a+1)x,
∴ax2-(2a+1)x+2<0,
由于a>0,且方程ax2-(2a+1)x+2=0的两根为x=2或x=
| 1 |
| a |
∴当
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
当
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
点评:本题考查函数的恒成立问题与抽象函数的应用,关键是用赋值法求出f(0),进而来判断函数的奇偶性.

练习册系列答案
相关题目
 如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在空白区域的概率为( )
如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在空白区域的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
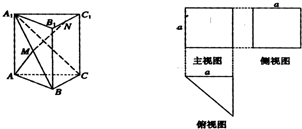 一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点.
一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点.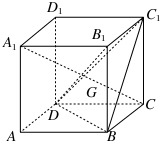 如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,