题目内容
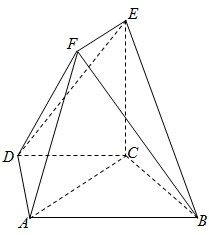 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
(Ⅰ)求证:BC⊥AF;
(Ⅱ)试判断直线DF与平面BCE的位置关系,并证明你的结论.
考点:直线与平面平行的判定,平面与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)取AB中点H,连结CH,先证明出四边形AHCD为平行四边形,推断出AD=HC=
AB,证明出BC⊥AC,进而根据线面垂直的判定定理推断出BC⊥平面ACEF,最后根据线面垂直的性质推断出BC⊥AF.
(Ⅱ)取AC的中点M,连接DM,FM,先证明出FM∥EC,根据面面平行的判定定理推断出平面BCE∥平面DMF,进而根据面面平行的性质推断出DF∥平面BCE.
| 1 |
| 2 |
(Ⅱ)取AC的中点M,连接DM,FM,先证明出FM∥EC,根据面面平行的判定定理推断出平面BCE∥平面DMF,进而根据面面平行的性质推断出DF∥平面BCE.
解答:
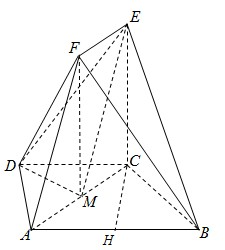 (Ⅰ)证明:取AB中点H,连结CH,
(Ⅰ)证明:取AB中点H,连结CH,
∵底面ABCD是梯形,且AD=DC=CB=
AB,
∴CD=AH,CD∥AH,
∴四边形AHCD为平行四边形,
∴AD=HC=
AB,
∴∠ACB=90°,
∴BC⊥AC,
∵平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF,
而AF?平面ACEF,
故BC⊥AF.
(Ⅱ)DF∥平面BCE,以下证明:
取AC的中点M,连接DM,FM.
∵在平面ABCD中,DM⊥AC,BC⊥AC,
∴DM∥BC.
∵在直角梯形ACEF中,EF
CM,
∴FM∥EC.
∵BC,CE?平面BCE,BC∩CE=C,DM,MF?平面DMF,DM∩MF=M,
∴平面BCE∥平面DMF,DF?平面DMF,
∴DF∥平面BCE.
 (Ⅰ)证明:取AB中点H,连结CH,
(Ⅰ)证明:取AB中点H,连结CH,∵底面ABCD是梯形,且AD=DC=CB=
| 1 |
| 2 |
∴CD=AH,CD∥AH,
∴四边形AHCD为平行四边形,
∴AD=HC=
| 1 |
| 2 |
∴∠ACB=90°,
∴BC⊥AC,
∵平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF,
而AF?平面ACEF,
故BC⊥AF.
(Ⅱ)DF∥平面BCE,以下证明:
取AC的中点M,连接DM,FM.
∵在平面ABCD中,DM⊥AC,BC⊥AC,
∴DM∥BC.
∵在直角梯形ACEF中,EF
| ||
. |
∴FM∥EC.
∵BC,CE?平面BCE,BC∩CE=C,DM,MF?平面DMF,DM∩MF=M,
∴平面BCE∥平面DMF,DF?平面DMF,
∴DF∥平面BCE.
点评:本题主要考查了线面平行的判定定理和性质以及线面垂直的判定定理及性质的应用.考查了学生综合运用立体几何基础知识的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知以原点O为圆心的单位圆上有一质点P,它从初始位置P0(
,
)开始,按逆时针方向以角速度1rad/s做圆周运动.则点P的纵坐标y关于时间t的函数关系为( )
| 1 |
| 2 |
| ||
| 2 |
A、y=sin(t+
| ||
B、y=sin(t+
| ||
C、y=cos(t+
| ||
D、y=cos(t+
|
 从全校参加期末考试的试卷中,抽取一个样本,考察成绩(均为整数)的分布,将样本分成5组,绘成频率分布直方图,如图所示.图中从左到右各小组的小矩形的高之比为2:3:6:4:1,最右边的一组频数是5.
从全校参加期末考试的试卷中,抽取一个样本,考察成绩(均为整数)的分布,将样本分成5组,绘成频率分布直方图,如图所示.图中从左到右各小组的小矩形的高之比为2:3:6:4:1,最右边的一组频数是5.