题目内容
已知函数f(x)=ax2-4x+b,(a∈R,b∈R)
(1)若函数f(x)有最小值3,求f(1)+2a的最小值;
(2)若b=-4a,解关于x的不等式f(x)>-8.
(1)若函数f(x)有最小值3,求f(1)+2a的最小值;
(2)若b=-4a,解关于x的不等式f(x)>-8.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据函数的最小值得出a和b的关系式,代入f(1)中,利用基本不等式求得f(1)+2a的最小值.
(2)把问题转化为解不等式ax2-4x-4a+8>0,对a进行分类讨论解不等式.
(2)把问题转化为解不等式ax2-4x-4a+8>0,对a进行分类讨论解不等式.
解答:
解:(1)函数f(x)有最小值3,
∴a>0,
=3,
∴b=
+3,f(1)=a-4+b=a+
-1,
∴f(1)+2a=3a+
-1≥2
-1=4
-1.
即f(1)+2a的最小值为4
-1.
(2)当b=-4a时,不等式f(x)>-8,可化为ax2-4x-4a+8>0,
①当a=0时,不等式即为-4x+8>0,x<2,
②当a>0时,原不等式即为(x-2)[x-(
-2)]>0,
当a>1时,x>2或x<
-2,
当a=1时,x≠2,
当0<a<1时,x>
-2或x<2,
③当a<0时,原不等式即为(x-2)[x-(
-2)],即
-2<x<2,
∴当a<0时不等式的解集为(
-2,2),
当a=0时,不等式的解集为(-∞,2),
当1>a>0时,原不等式解集为(
-2,+∞)∪(-∞,2)
当a=1时,原不等式解集为(x|x≠2,x∈R},
当a>1时,原不等式解集为(2,+∞)∪(-∞,
-2)
∴a>0,
| 4ab-16 |
| 4a |
∴b=
| 4 |
| a |
| 4 |
| a |
∴f(1)+2a=3a+
| 4 |
| a |
3a•
|
| 3 |
即f(1)+2a的最小值为4
| 3 |
(2)当b=-4a时,不等式f(x)>-8,可化为ax2-4x-4a+8>0,
①当a=0时,不等式即为-4x+8>0,x<2,
②当a>0时,原不等式即为(x-2)[x-(
| 4 |
| a |
当a>1时,x>2或x<
| 4 |
| a |
当a=1时,x≠2,
当0<a<1时,x>
| 4 |
| a |
③当a<0时,原不等式即为(x-2)[x-(
| 4 |
| a |
| 4 |
| a |
∴当a<0时不等式的解集为(
| 4 |
| a |
当a=0时,不等式的解集为(-∞,2),
当1>a>0时,原不等式解集为(
| 4 |
| a |
当a=1时,原不等式解集为(x|x≠2,x∈R},
当a>1时,原不等式解集为(2,+∞)∪(-∞,
| 4 |
| a |
点评:本题主要考查了二次函数的性质,分类讨论的思想和函数思想.考查了学生运算能力和逻辑思维能力.

练习册系列答案
相关题目
设集合A={(x,y)|
≤(x-2)2+y2≤m2,x,y∈R},B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B=∅,则实数m的取值范围是( )
| m |
| 2 |
A、
| ||||
B、0<m<2+
| ||||
C、m<2-
| ||||
D、m<
|
为得到函数y=cos(2x+3)的图象,只需将函数y=cos2x的图象( )
| A、向左平移3个长度单位 | ||
| B、向右平移3个长度单位 | ||
C、向左平移
| ||
D、向右平移
|
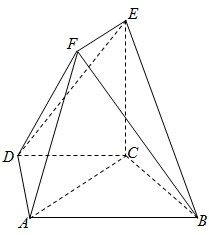 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=