题目内容
设a,b∈R,若函数f(x)=
(x∈R)是奇函数,则a+b= .
| 1+a•2x |
| 1+b•2x |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据定义在R上的奇函数满足图象过原点,且f(-x)=-f(x)恒成立,可求得a,b的值,进而得到答案.
解答:
解:∵函数f(x)=
(x∈R)是奇函数,
∴f(0)=
=0,
解得a=-1,
且f(-1)=
=-f(1)=-
,
解得:b=1,
此时f(x)=
,满足f(-x)=-f(x)恒成立,
故a+b=0,
故答案为:0
| 1+a•2x |
| 1+b•2x |
∴f(0)=
| 1+a |
| 1+b |
解得a=-1,
且f(-1)=
1-
| ||
1+
|
| 1-2 |
| 1+2b |
解得:b=1,
此时f(x)=
| 1-2x |
| 1+2x |
故a+b=0,
故答案为:0
点评:本题考查的知识点是函数奇偶性的性质,熟练掌握定义在R上的奇函数满足图象过原点,且f(-x)=-f(x)恒成立,是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
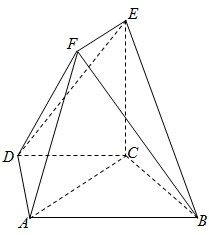 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=