题目内容
已知cos2θ-sin2θ=
,θ∈(0,
).
(1)求θ的值;
(2)若sinx=
,x∈(
,π),求cos(x+θ)的值.
| 1 |
| 2 |
| π |
| 2 |
(1)求θ的值;
(2)若sinx=
| 3 |
| 5 |
| π |
| 2 |
考点:二倍角的余弦,两角和与差的余弦函数
专题:三角函数的求值
分析:(1)已知等式左边利用二倍角的余弦函数公式化简,再利用特殊角的三角函数值即可求出θ的度数;
(2)由sinx的值,以及x的范围,利用同角三角函数间基本关系求出cosx的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
(2)由sinx的值,以及x的范围,利用同角三角函数间基本关系求出cosx的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答:
解:(1)∵cos2θ-sin2θ=cos2θ=
>0,θ∈(0,
),即2θ∈(0,
),
∴2θ=
,即θ=
;
(2)∵sinx=
,x∈(
,π),
∴cosx=-
=-
,
则cos(x+θ)=cosxcosθ-sinxsinθ=-
×
-
×
=-
.
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴2θ=
| π |
| 3 |
| π |
| 6 |
(2)∵sinx=
| 3 |
| 5 |
| π |
| 2 |
∴cosx=-
| 1-sin2x |
| 4 |
| 5 |
则cos(x+θ)=cosxcosθ-sinxsinθ=-
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
4
| ||
| 10 |
点评:此题考查了二倍角的余弦函数公式,两角和与差的余弦函数公式,熟练掌握公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的内角A,B,C所对的边分别为a,b,c,若c2<a2+b2+2abcos2C,则∠C的可能取值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
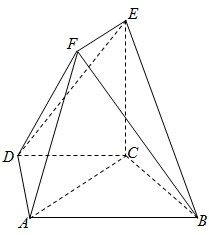 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=