题目内容

已知F1、F2分别为双曲线的左、右焦点，点P为双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）右支上的一点，满足
PF1
•
PF2
=0，且|PF1|=
3
|PF2|，则该双曲线离心率为
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的定义可知|PF2|-|PF1|=2a，进而根据|PF1|=
3
|PF2|，分别求得|PF2|和|PF1|，根据勾股定理建立等式求得a和c的关系，则离心率可得．
解答： 解：由
PF1
•
PF2
=0，可得PF1⊥PF2，
∵|PF1|=
3
|PF2|，|PF1|-|PF2|=2a，
∴|PF2|=（
3
+1）a，|PF1|=（3+
3
）a；
在RT△PF1F2中，|F1F2|2=|PF1|2+|PF2|2，
∴4c2=4（
3
+1）a2，解得e=
3
+1
故答案为：
3
+1．
点评：本题主要考查了双曲线的应用．考查了学生对双曲线定义和基本知识的掌握．
练习册系列答案
相关题目
已知函数f（x）=
3
（cos2x-sin2x）+2sinxcosx．
（1）求f（x）的最小正周期；
（2）求f（x）的单调递增区间．
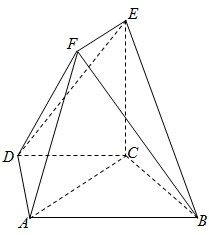如图，在多面体ABCDEF中，底面ABCD是梯形，且AD=DC=CB=
1
2
AB．直角梯形ACEF中，EF
∥
.
.
1
2
AC，∠FAC是锐角，且平面ACEF⊥平面ABCD．
（Ⅰ）求证：BC⊥AF；
（Ⅱ）试判断直线DF与平面BCE的位置关系，并证明你的结论．
已知函数y=xlnx+1
（1）求这个函数的导数；     
（2）求这个函数的图象在点x=1处的切线方程．
（1）已知a＞b＞c，且a+b+c=0，用分析法求证：
b2-ac
＜
3
a．
（2）f（x）=
1
3x+
3
，先分别求f（0）+f（1），f（-1）+f（2），f（-2）+f（3），然后归纳猜想一般性结论，并给出证明．
若点P（x，y）是不等式组
x+y≤3
x-y≥-1
x+3y≥3
表示的平面区域内的一点，点Q的坐标是（2，-1），O为坐标原点，则
OP
•
OQ
的最小值是
 
．
已知条件p：x＞a，条件q：x2+x-2＞0，若p是q的充分不必要条件，则实数a的取值范围是
 
．
已知P（x，y）为圆（x-1）2+（y-1）2=4上任意一点，则x+y的最大值为
 
．
函数y=
1
2-2-x
的定义域是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网