题目内容
已知以原点O为圆心的单位圆上有一质点P,它从初始位置P0(
,
)开始,按逆时针方向以角速度1rad/s做圆周运动.则点P的纵坐标y关于时间t的函数关系为( )
| 1 |
| 2 |
| ||
| 2 |
A、y=sin(t+
| ||
B、y=sin(t+
| ||
C、y=cos(t+
| ||
D、y=cos(t+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:先求出函数的周期,由周期求出ω,由特殊点的坐标求φ,可得函数的解析式.
解答:
解:设函数的解析式为y=sin(ωt+φ),t≥0,
∵函数的周期为
=2π,∴ω=1.
再根据函数的图象过点(0,
),可得sinφ=
,故可取φ=
,
故函数的解析式为y=sin(t+
),t≥0,
故选:A.
∵函数的周期为
| 2π |
| 1 |
再根据函数的图象过点(0,
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
故函数的解析式为y=sin(t+
| π |
| 3 |
故选:A.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求φ,属于基础题.

练习册系列答案
相关题目
用数学归纳法证明等式:1+2+3…+3n=
,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
| 9n2+3n |
| 2 |
| A、3k+1 |
| B、(3k+1)+(3k+2) |
| C、3k+3 |
| D、(3k+1)+(3k+2)+(3k+3) |
设集合A={(x,y)|
≤(x-2)2+y2≤m2,x,y∈R},B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B=∅,则实数m的取值范围是( )
| m |
| 2 |
A、
| ||||
B、0<m<2+
| ||||
C、m<2-
| ||||
D、m<
|
已知△ABC的内角A,B,C所对的边分别为a,b,c,若c2<a2+b2+2abcos2C,则∠C的可能取值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在复平面内,复数-2+3i对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的样本编号可能为( )
| A、5,10,15,20,25 |
| B、9,19,29,39,49 |
| C、2,13,24,35,46 |
| D、5,15,20,30,40 |
为得到函数y=cos(2x+3)的图象,只需将函数y=cos2x的图象( )
| A、向左平移3个长度单位 | ||
| B、向右平移3个长度单位 | ||
C、向左平移
| ||
D、向右平移
|
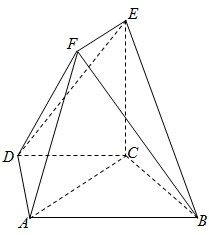 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=